我对于这是一个数学问题还是编程问题有些犹豫，但我怀疑一般数学家可能不太了解或关心这个特定范畴，而 Haskell 程序员可能会。
因此，我们知道 Hask 有积，多多少少（当然，这里我是在使用理想化的 Hask）。我想知道它是否有等化子（如果有，那么它将拥有所有有限极限）。
直觉上似乎不是这样，因为你不能像在集合中那样进行分离，所以子对象在一般情况下似乎很难构造。但对于您想出的任何特定情况，似乎您都可以通过计算在 Set 中的等化子并计数来进行测试（毕竟，每个 Haskell 类型都是可数的，每个可数集都同构于有限类型或自然数，而 Haskell 都具备这两种类型）。因此，我看不到如何找到反例。
现在，Agda似乎更有前途：在那里形成子对象相对容易。明显的sigma类型
Σ A (λ x → f x == g x) 是一个等值器吗？如果细节不起作用，它是否在道义上是一个等值器？简而言之，所提出的等式器并不完全是一个平衡器，但它的无关对应物却是如此。
Agda 中的等式器候选人看起来很好。那么让我们试试它。我们需要一些基本的工具。这里有我的 ASCII 拒绝依赖对类型和同质内延等性。
record Sg (S : Set)(T : S -> Set) : Set where
constructor _,_
field
fst : S
snd : T fst
open Sg
data _==_ {X : Set}(x : X) : X -> Set where
refl : x == x
这是两个函数的均衡器候选者
Q : {S T : Set}(f g : S -> T) -> Set
Q {S}{T} f g = Sg S \ s -> f s == g s
fst投影将Q f g发送到S。Q f g的一个元素是源类型的元素s和一个证明，即f s == g s。但这是否是等值器？让我们试着使它成为等值器。_o_ : {R S T : Set} -> (S -> T) -> (R -> S) -> R -> T
(f o g) x = f (g x)
f o h和g o h鉴别为同一函数的h : R -> S都必须通过候选的fst : Q f g -> S分解。我需要提供另一个组件u : R -> Q f g，并证明确实h可以分解为fst o u。这是图示：(Q f g , fst)是一个等价器，如果当图表在没有u的情况下交换时，有唯一的方法可以添加u使图表仍然保持交换。
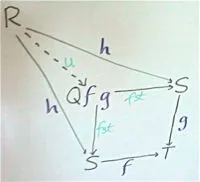
这里是中介u的存在。
mediator : {R S T : Set}(f g : S -> T)(h : R -> S) ->
(q : (f o h) == (g o h)) ->
Sg (R -> Q f g) \ u -> h == (fst o u)
mediator f g h q = (\ r -> (h r , ?0)) , ?1
?0 : f (h r) == g (h r)
?1 : h == (\ r -> h r)
?1 可以直接用 refl，因为 Agda 的定义相等性对于函数有 eta 规律。对于 ?0，我们有幸拥有 q。相等的函数保留应用。funq : {S T : Set}{f g : S -> T} -> f == g -> (s : S) -> f s == g s
funq refl s = refl
?0 = funq q r。 == 是內涵的，所以唯一性意味著只有一種實現中介映射的方式。但是，我們的假設也是內涵的... mediator 選擇的那一個。mediatorUnique :
{R S T : Set}(f g : S -> T)(h : R -> S) ->
(qh : (f o h) == (g o h)) ->
(m : R -> Q f g) ->
(qm : h == (fst o m)) ->
m == fst (mediator f g h qh)
qm进行替换并获得。mediatorUnique f g .(fst o m) qh m refl = ?
? : m == (\ r -> (fst (m r) , funq qh r))
这看起来很不错，因为Agda对记录有eta规则，所以我们知道
m == (\ r -> (fst (m r) , snd (m r)))
但是当我们尝试制作? = refl时，会出现投诉
snd (m _) != funq qh _ of type f (fst (m _)) == g (fst (m _))
这很烦人，因为身份证明通常都是唯一的。不过，你可以通过假设外延性并利用一些关于相等性的事实来解决这个问题。
postulate ext : {S T : Set}{f g : S -> T} -> ((s : S) -> f s == g s) -> f == g
sndq : {S : Set}{T : S -> Set}{s : S}{t t' : T s} ->
t == t' -> _==_ {Sg S T} (s , t) (s , t')
sndq refl = refl
uip : {X : Set}{x y : X}{q q' : x == y} -> q == q'
uip {q = refl}{q' = refl} = refl
? = ext (\ s -> sndq uip)
record Ex (S : Set)(T : S -> Set) : Set where
constructor _,_
field
fst : S
.snd : T fst
open Ex
新的候选人均衡器是
Q : {S T : Set}(f g : S -> T) -> Set
Q {S}{T} f g = Ex S \ s -> f s == g s
? = refl
被接受了！
所以，即使在内涵设置中，Eta定律和将字段标记为不相关的能力也给我们带来了等式器。
在这个构造过程中没有涉及不可判定类型检查。
Hask没有等式器。需要记住的一件重要事情是，思考类型（或任何类别中的对象）及其同构类实际上需要考虑箭头。你所说的关于底层集合的内容是正确的，但具有同构底层集合的类型并不一定是同构的。Hask和Set之间的一个区别在于，Hask的箭头必须是可计算的，并且对于理想化的Hask，它们必须是总的。
我花了一段时间尝试提出一个真正可靠的反例，并找到了一些参考资料表明这是不可能的，但没有证明。然而，我确实有一些“道德”反例，如果你愿意的话；我无法证明Haskell中不存在等式器，但它肯定似乎不可能存在！
f, g: ([Int], Int) -> Int
f (p,v) = treat p as a polynomial with given coefficients, and evaluate p(v).
g _ = 0
均衡器“应该”是所有对(p,n)的类型，其中p(n)=0，并且有一个将这些对注入([Int], Int)的函数。根据希尔伯特第十个问题，这个集合是不可判定的。我认为这应该排除它是Haskell类型的可能性，但我无法证明（可能存在某种奇怪的方式构造这种类型，没有人发现吗？）。也许我还没有连接一两个点——也许证明这是不可能的并不难？
假设你有一种编程语言。你有一个编译器，它接受源代码和输入，并产生一个函数，其固定点是输出。（虽然我们没有这样的编译器，但指定类似于这样的语义并不罕见）。所以，你有：
compiler : String -> Int -> (Int -> Int)
将其转换为函数（取消柯里化）
compiler' : (String, Int, Int) -> Int
并添加一个函数
id' : (String, Int, Int) -> Int
id' (_,_,x) = x
编译器'id的等式器将是源程序、输入和输出的三元组集合——这是不可计算的，因为编程语言是完全通用的。
选择您最喜欢的不可判定问题：它通常涉及决定对象是否是某个集合的成员。您经常有一个总函数，可以用来检查特定对象的属性。您可以使用此函数创建一个等式器，其中类型应为您的不可判定集合中的所有项目。那就是前两个示例的来源，还有很多。
我对Agda不太熟悉。我的直觉是，您的sigma类型应该是一个等式器：您可以将类型写下来，以及必要的注入函数，并且它看起来完全满足定义。但是，作为不使用Agda的人，我认为我没有资格检查细节。
然而，真正的实际问题是，类型检查该sigma类型并不总是可计算的，因此这样做并不总是有用的。在上面的所有示例中，您可以写下提供的Sigma类型，但是如果没有证明，您将无法轻松地检查某些内容是否属于该类型。
顺便提一下，这就是为什么Haskell不应该有等式器的原因：如果有的话，类型检查将是不可判定的！依赖类型是使所有事情运转的关键。它们应该能够在其类型中表达有趣的数学结构，而Haskell则不能，因为其类型系统是可判定的。因此，我自然会期望理想化的Agda具有所有有限极限（否则我会感到失望）。其他依赖类型的语言也是如此；例如，Coq肯定应该拥有所有极限。