我的教授刚刚教了我们这样一个规则:任何将输入长度减半的操作,复杂度都可以用 O(log(n)) 来近似表示。为什么不是O(sqrt(n))呢?这两个复杂度不是等价的吗?
它们并不相等:sqrt(N) 的增长速度比 log2(N) 快得多。不存在常数C,使得对于所有大于某个最小值的N值,你都有sqrt(N) < C.log(N)。
一个简单的理解方法是,log2(N)将会是接近于N的(二进制)位数,而sqrt(N)将会是一个数字,其本身的位数只有N的一半。或者,用一个等式来说明:
log2(N) = 2log2(sqrt(N))
所以,你需要取sqrt(N)的对数(!)来将其降到与log2(N)的同一复杂度级别。
例如,对于一个有11个二进制数位的二进制数,0b10000000000 (=210),平方根是0b100000,但对数仅为10。
2
log(N) 的值接近于 N (二进制)位数的数量,而 sqrt(N) 的值则为拥有 N 数字一半位数的数字。 - Weishi Zlim {n->inf} log n / sqrt(n) = (inf / inf)
lim {n->inf} log n / sqrt(n) = (inf / inf)
= lim {n->inf} 1/n / 1/(2*sqrt(n)) (by L'Hospital)
= lim {n->inf} 2*sqrt(n)/n
= lim {n->inf} 2/sqrt(n)
= 0 < inf
请参考https://en.wikipedia.org/wiki/Big_O_notation获取关于O(.)的备选定义,由此我们可以得出log n = O(sqrt(n))。同时比较下面这些函数的增长情况,对于所有n>0,log n始终被sqrt(n)上界限制。
只需比较这两个函数:
sqrt(n) ---------- log(n)
n^(1/2) ---------- log(n)
Plug in Log
log( n^(1/2) ) --- log( log(n) )
(1/2) log(n) ----- log( log(n) )
显然有:const . log(n) > log(log(n))
1
@trincot在他的答案中提供了一个很好的例子进行了解释。我想补充一点。你的教授教你那样做是因为……
any operation that halves the length of the input has an O(log(n)) complexity
同时也是真的,
any operation that reduces the length of the input by 2/3rd, has a O(log3(n)) complexity
any operation that reduces the length of the input by 3/4th, has a O(log4(n)) complexity
any operation that reduces the length of the input by 4/5th, has a O(log5(n)) complexity
So on ...
即使输入长度减少了(B-1)/Bth,对于所有的长度缩减都适用。此时,它的复杂度为O(logB(n))
N:B: O(logB(n))表示以B为底的n的对数。
O(n**k) > O(log(n, base))
对于任何
k>0和base>1(在sqrt的情况下,k=1/2)。当谈论
O(f(n))时,我们想要调查大的n的行为,极限是一个好的手段。假设两个大O是等价的: O(n**k) = O(log(n, base))
这意味着有一个有限的常数
C,使得 O(n**k) <= C * O(log(n, base))
从足够大的 n 开始;换句话说,(log(n, base) 在大的 n 时不是 0,两个函数都是连续可微的):
lim(n**k/log(n, base)) = C
n->+inf
为了找出极限的值,我们可以使用L'Hospital's Rule,即对分子和分母取导数并将它们相除:
lim(n**k/log(n)) =
lim([k*n**(k-1)]/[ln(base)/n]) =
ln(base) * k * lim(n**k) = +infinity
因此我们可以得出结论,不存在一个常数C,使得O(n**k) < C*log(n, base)成立,换句话说
O(n**k) > O(log(n, base))
1
sqrt(n) 比 lgn(base2) 快增长,您可以取第二个函数除以第一个函数的极限,并证明它在 n 趋近于无穷大时趋近于0。lim(n—>inf) of (lgn/sqrt(n))
应用洛必达法则:
= lim(n—>inf) of (2/(sqrt(n)*ln2))
由于随着 n 的增加,sqrt(n) 和 ln2 会无限增加,而2是一个常数,这证明了
lim(n—>inf) of (2/(sqrt(n)*ln2)) = 0
原文链接
- 相关问题
- 3 大O符号计算,O(n) * O(log n) = O(n log n)。
- 11 O(n log log n) 时间复杂度
- 23 O(n log n)和O(log n)有什么不同?
- 3 使用O(n log n) 或 O(log n)复杂度的Java程序
- 3 复杂度 O(log(n) + log(n/2) + log(n/4) + log(n/8) + ... + log(2)) 是否等于 O(log(n))?
- 5 O(n) + O(n log n) 是否等于 O(n log n)?
- 7 复杂度为O(logn)和O(log(sqrt(n)))之间的区别。
- 17 O(n log n)时间复杂度和O(1)空间复杂度的算法与O(n)时间复杂度和O(n)空间复杂度的算法比较。
- 5 O(n)是否大于O(2^log n)?
- 151 O(1) 复杂度算法的例子、O(n log n) 复杂度算法的例子和 O(log n) 复杂度算法的例子

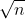
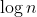
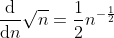
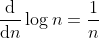
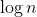
log(n)和sqrt(n)的图形,最高到n==1000,看看它们是否等价,无论您对此的意思是什么。 - High Performance Mark