我尝试使用scikit-learn库中的线性判别分析来对具有超过200个特征的数据进行降维。但是我在LDA类中找不到
我想问一下,如何从LDA域中的一个点重构原始数据?
根据@bogatron和@kazemakase的答案进行编辑:
我认为术语“原始数据”是错误的,而应该使用“原始坐标”或“原始空间”。我知道如果没有所有PCA,我们无法重构原始数据,但是当我们构建形状空间时,我们通过PCA的帮助将数据投影到较低的维度。 PCA尝试用仅2或3个组件解释数据,这些组件可以捕获大部分数据的方差,如果我们基于它们重构数据,它应该显示导致此分离的形状的部分。
我再次检查了scikit-learn LDA的源代码,发现特征向量存储在
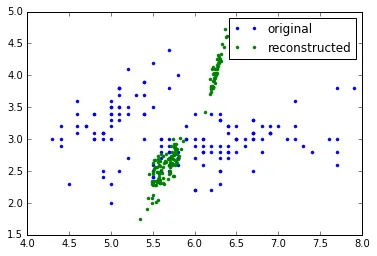
这里有两个图像,分别从[4.28, 0.52]和[0, 0]点重构而来:
inverse_transform函数。我想问一下,如何从LDA域中的一个点重构原始数据?
根据@bogatron和@kazemakase的答案进行编辑:
我认为术语“原始数据”是错误的,而应该使用“原始坐标”或“原始空间”。我知道如果没有所有PCA,我们无法重构原始数据,但是当我们构建形状空间时,我们通过PCA的帮助将数据投影到较低的维度。 PCA尝试用仅2或3个组件解释数据,这些组件可以捕获大部分数据的方差,如果我们基于它们重构数据,它应该显示导致此分离的形状的部分。
我再次检查了scikit-learn LDA的源代码,发现特征向量存储在
scalings_变量中。当使用svd求解器时,无法反转特征向量(scalings_)矩阵,但是当我尝试使用矩阵的伪逆时,我可以重构形状。这里有两个图像,分别从[4.28, 0.52]和[0, 0]点重构而来:
我认为,如果有人深入解释LDA逆变换的数学限制,那将是非常好的。
![from [ 4.28, 0.52]](https://istack.dev59.com/msyas.webp)
![from [0, 0]](https://istack.dev59.com/Ejpt2.webp)