你好,首先我必须说这是一个非常有趣和有趣的问题,而且在堆叠时我没有想到过,尽管在15个球中一些额外的移动并不重要。
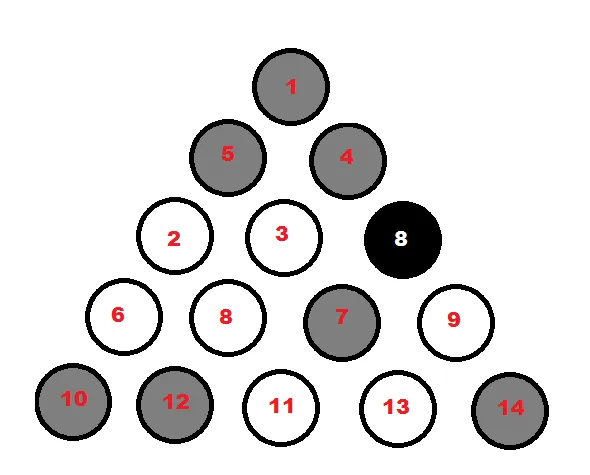
从堆叠描述和图像中,我们得到以下规则:
- 角落总是相同类型的
- 每个侧面的中间总是与角落相同类型
- 接触角落的每组2个球总是相同类型(与角落相反的类型)
- 内三角形总是有8个球,条纹和实心(8个球在顶部)
- 在两侧,彼此靠近的球总是交替类型
如@DPenner在引理1中所述,旋转不是必需的,因为它们可以被交换替代,前提是成本相同。如果您是Rubick的粉丝,并选择使用它们,您只需要一个。
无法在少于4次交换中解决!(始终)
您的示例图像最好证明这一点,无论如何计算,您都需要将6个颜色球从其位置上卸下,并将8ball =>那是3.5次交换,因为一个交换需要2个球,让我们将其四舍五入为4次交换。
这是为什么?
因为它不符合所有规则:
[5,1,4] [2,6] [11,13] [10,12] 不能彼此靠近(违反了5)8ball在侧面而不是在中间三角形中(违反了4)[5,4] [6,12] [13,9] 不是所有相同类型(违反3),此外,在[1,5,4]的情况下,该集不与角落相反(再次违反3)[2]和[11]与角落不是相同类型(违反2)
算法
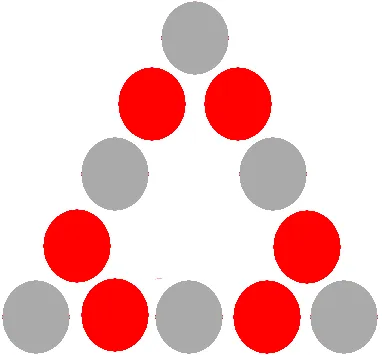
第一步:修复8ball
将8ball交换到其位置。无论如何都需要它在那里。
这是旋转的唯一机会(如果8ball从内三角形开始,但位置不正确)
计数红色位置中最多的相同类型的球。
最高计数球留下,其余的点必须被交换出去。
IF count is 3 {
#inside triangle will choose
IF inside triangle has 2 of a kind, that type stays (in the red spots)
ELSE pick random
}
开始交换:
- 先交换角落的球(选择需要更换的一个球,找到对面的一个在角落的球)
- 再交换中间的球(选择需要更换的一个球,找到对面的一个在边上中间的球)
- 如果角落和中间的球已经交换完了,最后一个交换在内部三角形里
示例演示:
swap 8 with 3 #move1
count[stripe]=3 [6,13,9]
count[solid]=3 [5,4,12]
highest count=3, checking inside, inside is correct, random pick: stripes stay
Pick 5, corners() correct, swap with middles(2) #move2
Pick 4, corners() correct, swap with middles(11) #move3
Pick 12, corners() correct, swap with middles(3) #move4
Done.
如果随机选择,会选择实心保留:
Pick 6, swap with corners(10)
Pick 13, swap with corners(1)
Pick 9, swap with corners(14)
Done.
Demo2:
将3替换为7,用球号15代替“白球8号”
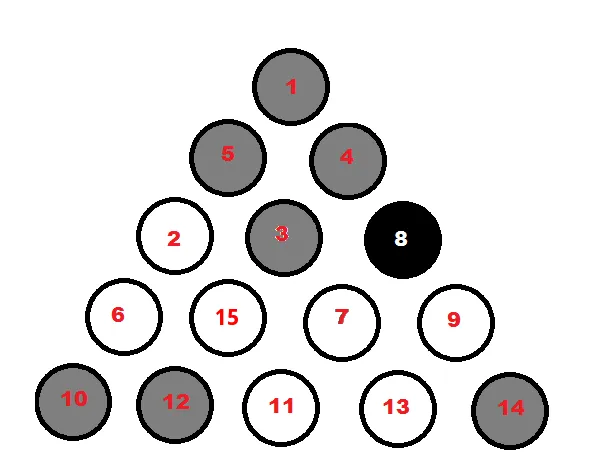
swap 8 with 3 #move1
count[stripe]=3 [6,13,9]
count[solid]=3 [5,4,12]
highest count=3, checking inside, inside has 2 of a kind(stripes) => stripes stay
Pick 5, corners() correct, swap with middles(2) #move2
Pick 4, corners() correct, swap with middles(11) #move3
Pick 12, corners() correct, swap with middles(15) #move4
Done.
玩得开心!
PS:你可能也会喜欢算法变体#2,它计数灰色位置,但我觉得在实际场景中使用红点更容易。