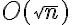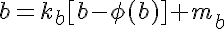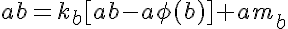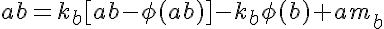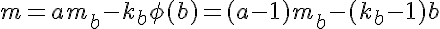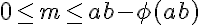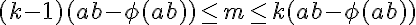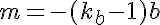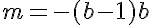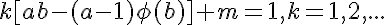欧拉计划问题245

Question

欧拉计划问题245

pythonalgorithmmath

8

我现在正在处理问题245，但遇到了一些问题。我已经做了一些工作，但感觉还没有朝着解决问题迈出实质性的步伐。以下是目前的进展：

我们需要找到n=ab，其中a和b为正整数。我们还可以假设gcd(a,b)=1，而不失一般性，因此phi(n)=phi(ab)=phi(a)phi(b)。

我们正在尝试解决：

$\frac{n-\phi(n)}{n-1}=\frac1k$

$\frac{n-1}{n-\phi(n)}=k$

因此：

$n\equiv1\ (\text{mod }n-\phi(n))$

在这一点上，我认为实际查看这些数字的分布将是一个好主意。我编写了一个蛮力程序，用于查找所有小于10⁴的(合数)解：

15, 85, 255, 259, 391, 589, 1111, 3193, 4171, 4369, 12361, 17473, 21845, 25429, 28243, 47989, 52537, 65535, 65641, 68377, 83767, 91759

重要的是，看起来问题所要求的不到10^11的限制下，似乎不会有太多解。我发现最有趣/有用的部分是即使对于很大的n值，k也相当小。实际上，最大的k只有138。（另外，似乎k总是偶数。）

考虑到这一点，我猜测可以考虑每个k值并找出与该k值相对应的n值。

回到原方程，注意它可以重写为：

$\frac{\phi(n)-1}{n-1}=\frac{k-1}k$

由于我们知道k：

$k\cdot\phi(n)\equiv k\ (\text{mod }n-1)$

这就是我目前的进展；我仍在追求一些路线，但我想知道我是否错过了重点！通过暴力方法，我已找到了10⁸的总和，即5699973227（仅有237个n的解决方案）。

我基本上没有想法了；有人能给一些提示吗？

更新：许多人已经完成了大量工作，我们一起证明了几件事情。以下是列表：

n始终为奇数，k始终为偶数。k≤10^5.5。n必须是无平方因子的。

我已经找到了n=pq（2个质因数）且p>q的每个解决方案。我使用了这样一个事实：对于两个质数q=k+factor(k^2-k+1)和p=k+[k^2-k+1]/factor(k^2-k+1)。我们还知道对于2个质数k

对于具有2个或更多质因数的n，n的所有质数均大于k。

- PythonPower

1

如果你不了解术语，这个欧拉问题会让人感到困惑；在＃243中更好地定义了它们：http://projecteuler.net/index.php?section=problems&id=243。 - Glenn

1

我能够弄清楚一点：k 必须整除 n-1（从你的第一个方程中推导出来，所以在一个全整数表达式中有一个类似于(n-1)/k的项），k 不一定（必须）整除 phi(n)（在你的穷举列表中有反例），而且 n 必须是奇数（因此 k 是偶数）（很容易证明 (k-1)n = k phi(n) - 1；将这个表达式对2取模并记住/重新证明 phi(n) 对于 n > 2 总是偶数）。我不知道接下来该怎么做了，现在我只有这么多时间可以用。 - kquinn

52

我认为在Stack Overflow上讨论并不符合欧拉计划的精神。 ;) - leif

谢谢kquinn。你关于k除以n-1的说法是正确的。这意味着n = jk+1 = ab，其中j为某个整数。我得出门了，稍后会继续跟进。谢谢！ - PythonPower

1

我仔细检查了我上面发布的内容，它是正确的。你用来得出相同问题的方程可能正确，也可能不正确，我还没有能够检查。还有一些你可能会发现有用的东西：我证明了k和phi(n)是彼此的模反元素，模n。这是另一个从(k-1)n = k phi(n) - 1显然得出的结果。 - kquinn

显示剩余4条评论

6个回答

4

让我继续Jug的思路，但采用稍微不同的方法。目标仍然是找到具有两个不同因子n=pq的数字。正如你所指出的，我们要寻找满足n-phi(n)可整除n-1的数字。也就是说，如果n=pq，则意味着我们要寻找p、q，使得

  p+q-1 divides pq-1

假设我们固定p，要寻找满足上述方程的所有质数q。这个方程看起来不太容易解决，因此下一步是尽可能消除q的影响。特别地，我们使用了如果a整除b，那么a也整除b+ka（其中k为任意整数）这个性质。因此，

  p+q-1 divides pq - 1 - p(p+q-1)

简化后，此条件可表示为：

  p+q-1 divides p^2 - p + 1.

我们可以假设p是n的较小质因数。那么p小于10^11的平方根。因此，通过迭代所有小于10^11平方根的质数p，可以找到所有有两个因子的数字，然后找到p^2-p+1的除数，解出q并检查q是否为质数且pq是问题的解。当然，这仍然留下了具有超过两个质因数的整数。在这里，一个类似的方法也适用，但需要进一步优化。

我无法回答的一个问题是：为什么这个问题被表述得如此复杂。作者难道不是只要求出当n-phi(n)除以n-1时的合成整数之和吗？所以也许我错过了一个重要的提示。

现在已知具有两个质因数的解决方案，我将尝试找到一个可能的算法来找到具有超过两个质因数的解决方案。目标是找到一个算法，给定一个复合整数m，找到所有的质数q，使得mq是解决方案。也就是说，q必须满足

  mq - phi(mq) divides mq - 1.

Let

  F = mq - phi(mq).

当然，接下来的内容是关于IT技术的。

  F = (m-phi(m)) q + phi(m).

在两个质因数的情况下，可以通过从上述方程的左边消去q来找到F的条件。由于F除以mq-1，它也除以

  (m-phi(m))(mq - 1)

因此也

  m F - (m-phi(m))(mq - 1)  = m phi(m) + m - phi(m).

因此，通过找到m phi(m) + m - phi(m)的所有因子F，并检查(F - phi(m))/ (m - phi(m))是否为质数，可以找到给定m的所有解mq。由于只有满足以下条件的因子F才能：

 F == phi(m) (mod m - phi(m))

可以导致新的解决方案，这个事实有时可以用来优化m phi(m) + m - phi(m)的因式分解。

- Accipitridae

我并没有完全按照那种方式做，但我已经找到了所有的2质数解。至于复杂的问题，我认为这适用于许多问题，比如241，其中包含无关信息！ - PythonPower

很棒的工作。那肯定已经接近了。然而，像3902867 = 53x211x349这样的数字仍然会被忽略。这是因为没有任何合数可以通过添加质数来扩展它。 - PythonPower

3

不完全是。当输入m = 53*211时，我的程序确实找到了q = 349。问题在于找到一个好的标准来选择需要测试的m的值。例如，如果m和phi(m)不互质，则无需测试它们。我可以假设q是最大的质因数，因此我不需要测试所有小于10^11的m，但仍可能是一个很大的数字。 - Accipitridae

1

实际上，10^11 > n = pqr > p^3 意味着 p < 10^(11/3) < 4642。这很小。而且我们有 q < sqrt(10^11/p) < 10^5.5... 好吧，它不是那么小，但可能可行。对我来说，真正的问题似乎是 m phi(m) + m - phi(m) 太大了，无法分解。 - ShreevatsaR

哦，顺便说一句，摆脱 q 的操作很棒，真聪明！ :) - ShreevatsaR

显示剩余3条评论

3

用质数的乘积进行筛选。我的做法是首先检查每个2个质数的乘积；存储那些成功的乘积。然后使用已存储的乘积，检查具有更多质数的乘积（在您的暴力方法中显示了一个包含2个质数的子集）。使用这些存储的乘积，并再次尝试4个质数、5个质数等。

唯一的缺点是你需要一个好的筛法或质数列表。

这里是N <=（10^7）的一些列表：

2 个质数 15、85、259、391、589、1111、3193、4171、4369、12361、17473、25429、28243、47989、52537、65641、 68377、83767、91759、100777、120019、144097、186367、268321、286357、291919、316171、327937、346063、353029、360301、404797、406867、524851、531721、558013、563767、633727、705667、738607、910489、970141、1013539、1080769、1093987、1184233、1185421、1223869、1233823、1261807、1264693、1455889、1487371、1529641、1574383、1612381、1617379、1657531、1793689、2016379、2095087、2130871、2214031、2299459、2500681、2553709、2609689、2617963、2763697、3047521、3146677、3397651、3514603、3539017、3820909、3961219、4078927、4186993、4197901、4499707、4552411、4935883、4975687、5103841、5299351、5729257、5829877、5864581、6017299、6236401、6802531、6856609、8759011、9059233、9203377、9301603、9305311、9526747、9536899、9583279、9782347、9900217 3 个质数 255、21845、335923、3817309 4 个质数 65535 5 个质数 83623935

- xharfire

我能看到的唯一问题是计算所有的2个质数乘积。然而，可以证明如果n=pq，则(pq-1)/(p+q-1)=k，这是我可以研究的。非常感谢！ - PythonPower

1

好的，我尝试了你说的方法，但是像3902867这样的数字= 53x211x349找不到。不过，我可以扩展我用于查找2个质数的方法来查找更多的质数 - 我会试一试。 - PythonPower

1

对于这个问题没有直接的帮助，但也许对未来的数学项目有趣：不要使用WolframAlpha分析序列，我建议在research.att.com上使用"整数序列在线百科全书"。

祝你解决所有欧拉问题愉快！

- someone

OEIS已经迁移。该链接不再有效。现在请使用此链接：https://oeis.org/A160599 - Stefan Gruenwald

1

为了不泄露太多，我建议两件事情：

通过暴力分析你生成的数字序列：它们都有一个共同的特征。如果你找到了它，那么你就有可能通过暴力破解来解决问题。
寻找更复杂的因数分解算法。或者更好的方法是：不要从数字中找因数，而是从因数中构建数字...

编辑：你将发现的模式只会增加你的理解，并希望向您展示如何通过适当操作分析表达式来获得相同数量的知识。如果不知道该模式，恐怕没有解决方案的路径。此外，这可能是最难的欧拉计划问题之一，因此您无需担心在大量努力和辛勤工作的情况下找到解决方案...

- user91494

不太理想，因为我想要的是理解而不是侥幸猜测！ - PythonPower

这更接近我想做但无法实现的内容。 - PythonPower

0

我还没有找到完整的解决方案，但我想分享一下我的想法。也许有人可以帮忙。

我认为应该尝试将问题简化为

_{(来源: texify.com)}

复杂度。以下事实可用于使搜索更有效：

任何解决方案都必须是奇数
任何解决方案都必须是不同质数的倍数（不允许平方数因子）

其他人已经指出了这些问题，并且只使用欧拉函数的基本属性就可以轻松证明它们。

我将从分析所有素数和合数开始，直到sqrt(10^11)。这不是一个大任务，所需时间应该远低于1分钟的要求。所有在平方根以上的解决方案都是以下形式：

a*b, where at least one of a,b < sqrt(10^11)

在迭代范围0..sqrt(10^11)时，我将搜索迭代中的数字的倍数作为解。我只会处理将平方根以下的数字与单个质数相乘的情况。通过这种方式获得的解集将是两个质因子解集的超集。仍然不是完整的解集，因为形式为p1p2p3的解，其中p1p2、p2p3和p1p3> sqrt(10^11)将无法找到。

让b为平方根以下的数字，a为要乘以它的质数。

_{(来源: texify.com)}

我们有:

_{(来源：texify.com)}

基于以下事实

phi(a) = a - 1 and phi(a)*phi(b) = phi(a*b) if a, b coprime

我们有

_{(来源：texify.com)}

右侧的 '取模' 部分可以写成：

_{(来源: texify.com)}

让我暂时接受这个

_{(来源: texify.com)}

然后我可以解出上述方程，令m=1，验证结果是否为质数，然后我将得到唯一的解，即b的倍数。如果m不在实际模数的范围内，则需要为不同的k值解决该方程：

_{(来源: texify.com)}

（k 值必须受到某种限制）或证明在这种情况下将会有一个更高的 b < sqrt(10^11) 来弥补这一点。

b 为质数或合数且 mb = 0 时存在特殊情况：

_{(来源: texify.com)}

这可以计算出来。对于一个质数 b：

_{(来源: texify.com)}

我需要找到一个质数 a，满足以下方程式：

_{(来源: texify.com)}

例如，令b=3，phi(b)=2。

我需要解决：

k[3a-2(a-1)] - 6 = 1 => k(a + 2) = 5

对于k=1，a=7，a是质数（解决方案）对于所有其他的k值，上述方程式无法满足。

- kgiannakakis

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- Dmitri Farkov · Accepted Answer

9

Project Euler 不喜欢在公共论坛（如 StackOverflow）上讨论问题。所有任务都是独自完成的，如果你遇到问题，可以为特定的数学或编程概念寻求帮助，但不能决定询问如何解决手头的问题 - 这将削弱 Project Euler 的意义。

关键是要自己学习和想出解决方案，并学习新概念。

- Dmitri Farkov

7

从主页上看，“利用互联网研究问题是值得鼓励的，因为许多问题的表面下可能隐藏着数学上的宝藏。” - Marc Gravell

13

当你像PythonPower一样尝试了很多次并付出了许多努力，却仍然无法解决问题时，继续白费力气是没有意义的。你会到达一个阶段，自己已经学不到更多了。此时明智的做法是寻求帮助和学习，而不是放弃。 :P - ShreevatsaR

2

鼓励研究，而不是寻求解决难题的答案。我的意思是，通过阅读，你会意识到某个问题需要贝叶斯定理的知识，因此你会向人们寻求帮助来实现一个贝叶斯分类程序，而不是寻求整个难题的解决方案。 - Dmitri Farkov

7

他正在进行研究。他展示了他的工作，跟进了每一个暗示和猜测，并证明/推翻了它。在寻求帮助之前（甚至之后），你还期望他做什么？没有遇到新概念，又怎么能学习新概念呢？ - ShreevatsaR