从https://zh.wikipedia.org/wiki/快速选择算法中可以看到:
“然而,与快速排序递归进入两侧不同,快速选择仅递归进入一侧——具有所搜索元素的那一侧。这将平均复杂度从O(n log n)降低到O(n),最坏情况下为O(n^2)。”
我不明白为什么只查看一侧会将平均复杂度降低到O(n)?难道不应该是O(N/2 log N)吗,这仍然是O(N log N)。另外,最坏情况如何会是O(n^2)?
“然而,与快速排序递归进入两侧不同,快速选择仅递归进入一侧——具有所搜索元素的那一侧。这将平均复杂度从O(n log n)降低到O(n),最坏情况下为O(n^2)。”
我不明白为什么只查看一侧会将平均复杂度降低到O(n)?难道不应该是O(N/2 log N)吗,这仍然是O(N log N)。另外,最坏情况如何会是O(n^2)?
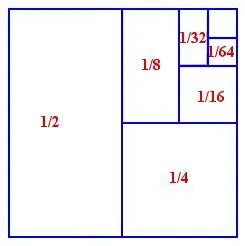
3.4n次比较才能找到中位数。尽管如此,你很可能会被一个几何级数所限制,其总和为O(n)。 - btillyO(1/n))。这就是为什么中位数对于快速选择来说是一个困难的情况。 - btilly3.4n的吗? - theprogrammer