简短回答:时间复杂度为
O(choose(N+k, N)),与
O(choose(N+k, k)) 相同。其中 choose 表示组合数。
这里是关于如何到达那里的详细回答。
你已经正确提出了基本问题版本。使用 k 个嵌套循环,你的复杂度将会是 O(N^k),随着 N 趋近无穷大。然而,由于 k 和 N 都在变化,行为更加复杂。
让我们考虑相反的极端情况。假设
N 固定,而
k 变化。
如果
N 为0,则您的时间是恒定的,因为最外层循环在第一次迭代时失败。如果
N = 1,则您的时间为
O(k),因为您只有一个选择并且每次都只有一个选择,通过所有嵌套级别。如果
N = 2,则会发生更有趣的事情,您一遍又一遍地进行嵌套,需要时间
O(k^N)。而一般来说,对于固定的
N,时间复杂度为
O(k^N),其中一个
k 的因素归因于遍历嵌套所需的时间,而
O(k^(N-1)) 的因素则归因于序列前进的位置。这是一个出乎意料的对称性!
现在,如果
k 和
N 都很大,会发生什么?那么它的时间复杂度是多少呢?好吧,这里有一些直觉。
我们能描述所有到达最内层循环的时间吗?可以!考虑有
k+N-1 个插槽,其中有
k 个被称为“进入了一个以上的循环”,而有
N-1 个被称为“我们将索引增加了1”。我断言如下:
- 这些与我们到达最内层循环的决策序列一一对应。可以通过查看哪些索引大于其他索引以及差值来看出。
- 在末尾的“进入一个以上的循环”条目是需要完成的工作,以到达本次迭代的最内层循环,但未导致任何其他循环迭代。
- 如果
1 < N,实际上需要多做一个唯一的工作才能到达终点。
现在这看起来有点混乱,但有一个意外地简化它的技巧。
这个技巧是这样的。假设我们取其中一个模式,并在最后一段“进入了一个循环”的条目中的某处插入了一个额外的“我们将索引增加1”。有多少种方法可以做到这一点呢?答案是我们可以将最后一个条目插入到该最后一段中的任意两个位置之间,包括开头和结尾,在所有条目数量上还有一种方法来做到这一点。换句话说,完成此迭代所需的唯一工作量与可以这样做的方式数量相匹配!
而这意味着总工作量与O(choose(N + k,N))成比例,也与O(choose(N + k,k))成比例。
值得知道的是,从正态近似到二项式公式,如果
N = k,那么结果为
O(2^(N+k)/sqrt(N+k)),这确实比多项式增长得更快。如果你需要更一般或更精确的近似,可以在
choose(N+k, N) = (N+k)! / ( N! k! )中使用
斯特林公式来近似阶乘。
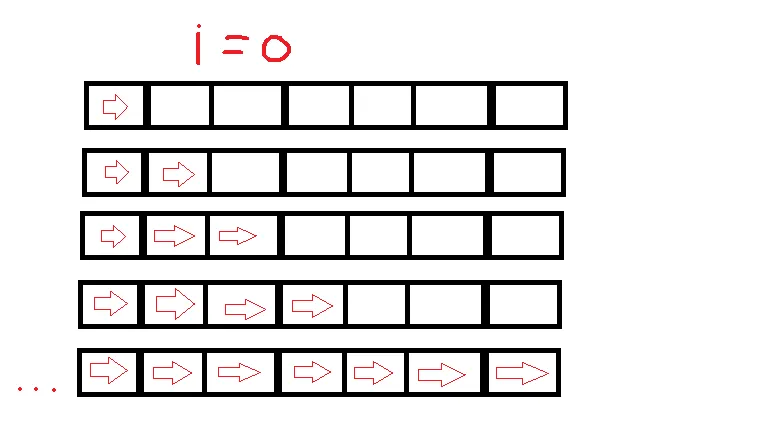
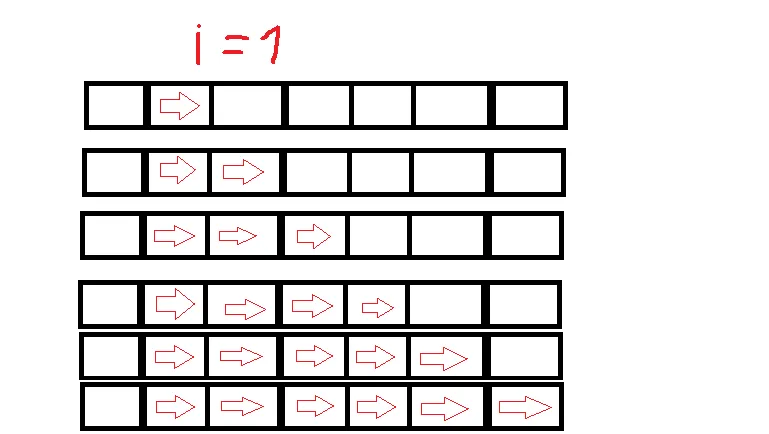 等等。
等等。
j++是正确的吗?原句为for(int start=i; start <= j; j++)。 - Jacob G.