一个带有嵌套迭代函数的递归算法的时间复杂度是多少？

Question

a)

void f(n){
  if(n<=1) return;
    else{
      g(n); //g(n) is O(N^2).
      f(n/2);
      f(n/2);
    } 
}

b)

void f(n){
  if(n<=1) return;
    else{
      g(n); //g(n) is O(N).
      f(n-1);
      f(n-1);
    } 
}

c)

void f(n){
  if(n<=1) return;
    else{
      g(n); //g(n) is O(N^2).
      f(n-1);
      f(n-1);
    } 
}

如何计算上述两个代码片段的O(n)复杂度？

a) 我得到了答案O(n^2)，因为每个f(n)递归调用自身两次。由于树的深度是LogN (n/2)，整体复杂度为O(n^2)，我是否应该忽略g(n)方法，因为它也是N^2的？

b) 由于树的深度为N，并且每个f(n)会递归调用自身两次。由于每个级别需要执行g(n)操作N次，所以我得到的答案是O(N.2^(N))。

c) 和b相同，但g(n)执行了N^2次 - 因此是O(N^2.2^(N))。

这个答案正确吗？

- Carrein

Answer 1

a) 递归公式如下所示。

如果您展开递归，我们有：

因此，我们想要计算最后一个等式，即：

由于上述等式的最后一部分是一个几何级数，我们有：

因此，递归是。

b) 方法与之前相同。

即：

因此，答案是。

c) 第三部分可以用相同的技巧解决。

PS：感谢Alexandre Dupriez的评论。

提示：如果您想更简洁地进行求和，可以参考下面Alexandre的评论。

- Bonje Fir

---

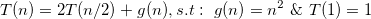
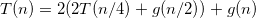
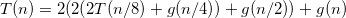
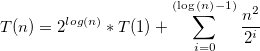
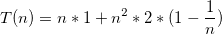
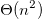
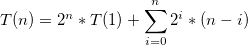
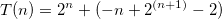
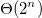
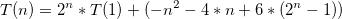
对于b)和c)，我认为复杂度是O(2^n) - 原因在于公式T(n) = 2^n + n.sum(2^i)的第二项中，n不能被分解为递增的和，即(b)为n + 2.(n - 1) + ... + 2^n，(c)为n^2 + 2.(n-1)^2 + ... + 2^n。 - Alexandre Dupriez

同意结果为theta(2^n) - 不确定如何简化求和？无论如何，我不会太在意得到部分和的精确表达式 - 我只是通过事实来证明sum(2^i.(n-i)) = 2^n.sum((n-i)/2^(n-i)) = 2^n.sum(k/2^k)，并且它发生了一般术语k/2^k的系列收敛于一个有限数（称之为c），由于有限和是递增的，所以sum(k/2^k) <= c，因此2^n.sum(k/2^k) <= c.2^n，由于我们可以找到另一个形式为d.2^n的下界，其中d < c，因此您获得了theta(2^n)。 - Alexandre Dupriez

我们还可以进一步推广到任何复杂度 g(n)，使得级数 sum(g(n)/2^n) 是有限的，这特别地让我们能够访问任何形式为 a1.n^p1.log(n)^q1 + a2.n^p2.log(n)^q2 + ... 的内容，其中 a1, a2, ...; p1, p2...; q1, q2... 等均可。 - Alexandre Dupriez

@AlexandreDupriez 优雅的简化。为了精确计算方程，我们可以将求和分解为sum(n*2^i) + sum(i*2^i)。第一部分是等比数列，第二部分在维基百科的求和页面中有指数项部分。此外，wolframalpha可以为我们计算它。我建议回答每个人都要读你的评论。谢谢。 - Bonje Fir

哦，我不知道WolframAlpha - 很好很强大的工具！谢谢。 - Alexandre Dupriez