解决这个问题的一种明显方法是按照预定顺序迭代所有字符串长度,更新每个字符串所在列的宽度,并在列宽总和超过终端宽度时停止。然后,对于减少的列数(或增加的行数,用于“向下排列”情况),重复此过程直到成功。这个预定顺序有三种可能的选择:
- 按行(先考虑第一行中的所有字符串,然后是第2、3行等)
- 按列(先考虑第一列中的所有字符串,然后是第2、3列等)
- 按值(按长度对字符串进行排序,然后按排序顺序迭代它们,从最长的开始)。
这三种方法都适用于“横向排列”子问题。但是对于“向下排列”子问题,它们的最坏时间复杂度都为O(n^2)。即使对于随机数据,前两种方法也显示出二次复杂度。按值的方法对于随机数据非常好,但很容易找到最坏情况:只需将短字符串分配给列表的前半部分,将长字符串分配给后半部分。
在这里,我描述了一种“向下排列”情况下没有这些缺点的算法。
不需要分别检查每个字符串长度,它使用范围最大查询(RMQ)在O(1)时间内确定每个列的宽度。第一列的宽度只是范围(0..num_of_rows)中的最大值,下一列的宽度是范围(num_of_rows..2*num_of_rows)中的最大值,以此类推。
为了在O(1)时间内回答每个查询,我们需要准备一个包含范围(0..2 k),(1..1 + 2 k)等最大值的数组,其中k是最大的整数,使得2 k 不大于当前行数。每个范围最大查询被计算为来自该数组的两个条目的最大值。当行数开始变得太大时,我们应该将这个查询数组从k更新到k + 1(每个这样的更新需要O(n)范围查询)。
以下是C ++14实现:
template<class PP>
uint32_t arrangeDownRMQ(Vec& input)
{
auto rows = getMinRows(input);
auto ranges = PP{}(input, rows);
while (rows <= input.size())
{
if (rows >= ranges * 2)
{
transform(begin(input) + ranges, end(input), begin(input),
begin(input), maximum
);
ranges *= 2;
}
else
{
uint32_t sum = 0;
for (Index i = 0; sum <= kPageW && i < input.size(); i += rows)
{
++g_complexity;
auto j = i + rows - ranges;
if (j < input.size())
sum += max(input[i], input[j]);
else
sum += input[i];
}
if (sum <= kPageW)
{
return uint32_t(ceilDiv(input.size(), rows));
}
++rows;
}
}
return 0;
}
这里的PP是可选的,对于简单情况,此函数对象不执行任何操作并返回1。
为了确定该算法的最坏时间复杂度,注意外部循环从rows = n * v / m(其中v是平均字符串长度,m是页面宽度)开始,并在最多rows = n * w / m(其中w是最大字符串长度)停止。"查询"循环中的迭代次数不超过列数或n / rows。将这些迭代次数相加得到O(n * (ln(n*w/m) - ln(n*v/m)))或O(n * log(w/v))。这意味着具有小常数因子的线性时间。
我们应该在此添加执行所有更新操作的时间,其复杂度为O(n log n),以获得整个算法的复杂度:O(n * log n)。
如果在进行查询操作之前不执行任何更新操作,则更新操作所需的时间以及算法复杂度将降至
O(n * log(w/v))。为了实现这一点,我们需要一些算法来用给定长度的子数组的最大值填充RMQ数组。我尝试了两种可能的方法,似乎
使用一对堆栈的算法稍微快一些。这是C++14的实现(输入数组的片段被用于实现两个堆栈,以降低内存要求并简化代码):
template<typename I, typename Op>
auto transform_partial_sum(I lbegin, I lend, I rbegin, I out, Op op)
{
auto sum = typename I::value_type{};
for (; lbegin != lend; ++lbegin, ++rbegin, ++out)
{
sum = op(sum, *rbegin);
*lbegin = op(*lbegin, sum);
}
return sum;
}
template<typename I>
void reverse_max(I b, I e)
{
partial_sum(make_reverse_iterator(e),
make_reverse_iterator(b),
make_reverse_iterator(e),
maximum);
}
struct PreprocRMQ
{
Index operator () (Vec& input, Index rows)
{
if (rows < 4)
{
return 1;
}
Index ranges = 1;
auto b = begin(input);
while (rows >>= 1)
{
ranges <<= 1;
}
for (; b + 2 * ranges <= end(input); b += ranges)
{
reverse_max(b, b + ranges);
transform_partial_sum(b, b + ranges, b + ranges, b, maximum);
}
reverse_max(b, b + ranges);
const auto d = end(input) - b - ranges;
const auto z = transform_partial_sum(b, b + d, b + ranges, b, maximum);
transform(b + d, b + ranges, b + d, [&](Data x){return max(x, z);});
reverse_max(b + ranges, end(input));
return ranges;
}
};
实际上,我们更有可能看到短单词而不是长单词。在英语文本中,较短的单词数量超过较长的单词,自然数的较短文本表示也更为普遍。因此,我选择(稍作修改的)字符串长度的几何分布来评估各种算法。
这里是整个基准测试程序(使用gcc的C++14)。旧版本的同一程序包含一些过时的测试和某些算法的不同实现:
TL;DR。以下是结果:
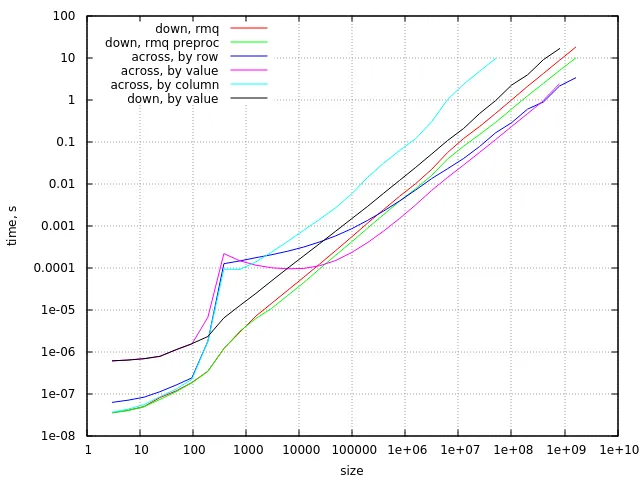
针对“横向排列”情况:
- “按列排列”的方法最慢
- “按值排列”的方法适用于n = 1000..500'000'000
- “按行排列”的方法更适用于小型和非常大型的数据
针对“纵向排列”情况:
- “按值排列”的方法可以,但比其他方法慢(使其更快的一种可能是通过乘法实现除法),并且它使用更多内存并具有二次最坏时间复杂度
- 简单的RMQ方法更好
- 预处理后的RMQ最佳:它具有线性时间复杂度,并且其内存带宽要求相当低。
还可以查看每个算法所需的迭代次数,这也很有趣。在此,所有可预测的部分都被排除在外(排序,求和,预处理和RMQ更新)。
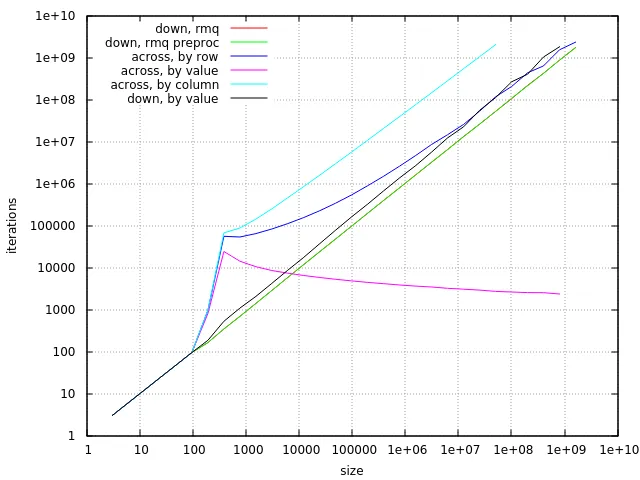


N/c个字符串),总共有O(N^2)个位置需要填充。 - NuclearmanO(N ^ 2),因此认为它就是这样。 - Nuclearmans的范围和m的上限是多少? - גלעד ברקן