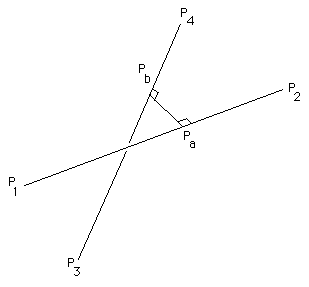
In what follows a line will be defined by two points lying on it, a point on line "a" defined by points P1 and P2 has an equation
Pa = P1 + mua (P2 - P1)similarly a point on a second line "b" defined by points P3 and P4 will be written as
Pb = P3 + mub (P4 - P3)The values of mua and mub range from negative to positive infinity. The line segments between P1 P2 and P3 P4 have their corresponding mu between 0 and 1.
There are two approaches to finding the shortest line segment between lines "a" and "b".
方法一:
方法二:The first is to write down the length of the line segment joining the two lines and then find the minimum. That is, minimise the following
|| Pb - Pa ||^2Substituting the equations of the lines gives
|| P1 - P3 + mua (P2 - P1) - mub (P4 - P3) ||^2The above can then be expanded out in the (x,y,z) components.
There are conditions to be met at the minimum, the derivative with respect to mua and mub must be zero. ...the above function only has one minima and no other minima or maxima. These two equations can then be solved for mua and mub, the actual intersection points found by substituting the values of mu into the original equations of the line.
这个方法是在Paul Bourke的网站上找到的,这是一个很好的几何资源。该网站已经重新组织,所以请向下滚动以找到相关主题。An alternative approach but one that gives the exact same equations is to realise that the shortest line segment between the two lines will be perpendicular to the two lines. This allows us to write two equations for the dot product as
(Pa - Pb) dot (P2 - P1) = 0 (Pa - Pb) dot (P4 - P3) = 0Expanding these given the equation of the lines
( P1 - P3 + mua (P2 - P1) - mub (P4 - P3) ) dot (P2 - P1) = 0 ( P1 - P3 + mua (P2 - P1) - mub (P4 - P3) ) dot (P4 - P3) = 0Expanding these in terms of the coordinates (x,y,z) ... the result is as follows
d1321 + mua d2121 - mub d4321 = 0 d1343 + mua d4321 - mub d4343 = 0where
dmnop = (xm - xn)(xo - xp) + (ym - yn)(yo - yp) + (zm - zn)(zo - zp)Note that dmnop = dopmn
Finally, solving for mua gives
mua = ( d1343 d4321 - d1321 d4343 ) / ( d2121 d4343 - d4321 d4321 )and back-substituting gives mub
mub = ( d1343 + mua d4321 ) / d4343
8
mua、mub、d1321等是什么?一条线段通常由两个向量定义。 - Skeeve我尝试了@Bill的答案,但并不总是有效,我可以解释一下原因。基于他代码中的链接。让我们举个例子,有这两条线段AB和CD。
A=(2,1,5), B=(1,2,5) and C=(2,1,3) and D=(2,1,2)
当你尝试获取交点时,它可能会告诉你它是点A(不正确)或者没有交点(正确)。这取决于你放置这些线段的顺序。
x = A+(B-A)s
x = C+(D-C)t
Bill解决了s,但从未解决过t。由于你希望交点位于两个线段上,所以s和t都必须来自区间<0,1>。在我的例子中,实际发生的是只有s来自该区间,而t为-2。A在由C和D定义的直线上,但不在线段CD上。
var s = Vector3.Dot(Vector3.Cross(dc, db), Vector3.Cross(da, db)) / Norm2(Vector3.Cross(da, db));
var t = Vector3.Dot(Vector3.Cross(dc, da), Vector3.Cross(da, db)) / Norm2(Vector3.Cross(da, db));
其中,da是B-A,db是D-C,dc是C-A,我只保留了Bill提供的名称。
然后,正如我所说,您必须检查s和t是否来自<0,1>,并且可以根据上述公式计算结果。
if ((s >= 0 && s <= 1) && (k >= 0 && k <= 1))
{
Vector3 res = new Vector3(this.A.x + da.x * s, this.A.y + da.y * s, this.A.z + da.z * s);
}
此外,Bills的回答还存在另一个问题,当两条线共线且存在多个交点时会出现除零的情况。你需要避免这种情况。
// This code in C++ works for me in 2d and 3d
// assume Coord has members x(), y() and z() and supports arithmetic operations
// that is Coord u + Coord v = u.x() + v.x(), u.y() + v.y(), u.z() + v.z()
inline Point
dot(const Coord& u, const Coord& v)
{
return u.x() * v.x() + u.y() * v.y() + u.z() * v.z();
}
inline Point
norm2( const Coord& v )
{
return v.x() * v.x() + v.y() * v.y() + v.z() * v.z();
}
inline Point
norm( const Coord& v )
{
return sqrt(norm2(v));
}
inline
Coord
cross( const Coord& b, const Coord& c) // cross product
{
return Coord(b.y() * c.z() - c.y() * b.z(), b.z() * c.x() - c.z() * b.x(), b.x() * c.y() - c.x() * b.y());
}
bool
intersection(const Line& a, const Line& b, Coord& ip)
// http://mathworld.wolfram.com/Line-LineIntersection.html
// in 3d; will also work in 2d if z components are 0
{
Coord da = a.second - a.first;
Coord db = b.second - b.first;
Coord dc = b.first - a.first;
if (dot(dc, cross(da,db)) != 0.0) // lines are not coplanar
return false;
Point s = dot(cross(dc,db),cross(da,db)) / norm2(cross(da,db));
if (s >= 0.0 && s <= 1.0)
{
ip = a.first + da * Coord(s,s,s);
return true;
}
return false;
}
思路是利用向量代数,使用“点”和“叉”操作,简化问题直至达到以下步骤:
a (V1 X V2) = (P2 - P1) X V2
并计算 a。
请注意,此实现不需要任何平面或轴作为参考。
6
如果(|(V1 X V2)| != 0),则a = |(P2-P1) X V2| / |V1 X V2|'a' 就是你的 t 值。 - randomraccoon同一网站还有关于3D情况的内容: "http://geomalgorithms.com/a07-_distance.html"
看起来Eberly写了一个回复: "https://www.geometrictools.com/Documentation/DistanceLine3Line3.pdf"
将这些东西放在这里是因为Google会指向geomalgorithms和这篇文章。
但是我害怕找到两个三维线段的交点。
我认为可以。你可以像在二维(或任何其他维度)中一样找到交点。唯一的区别是,结果线性方程组更可能没有解(表示这些线不相交)。
您可以手动解决常规方程并只使用您的解决方案,或通过编程解决它,例如使用 高斯消元法。
5
x,y和z)和两个未知数(u,v)。解决这个问题肯定不是一件容易的事情。 - Gravitonhttps://bloodstrawberry.tistory.com/1037 这篇博客是用Unity c#实现的。
Vector3 getContactPoint(Vector3 normal, Vector3 planeDot, Vector3 A, Vector3 B)
{
Vector3 nAB = (B - A).normalized;
return A + nAB * Vector3.Dot(normal, planeDot - A) / Vector3.Dot(normal, nAB);
}
(Vector3 point1, Vector3 point2) getShortestPath(Vector3 A, Vector3 B, Vector3 C, Vector3 D)
{
Vector3 AB = A - B;
Vector3 CD = C - D;
Vector3 line = Vector3.Cross(AB, CD);
Vector3 crossLineAB = Vector3.Cross(line, AB);
Vector3 crossLineCD = Vector3.Cross(line, CD);
return (getContactPoint(crossLineAB, A, C, D), getContactPoint(crossLineCD, C, A, B));
}
q = p2 + t * v2
其中,
t = dot(p1 - p2, v3) / dot(v2, v3)
而且
v3 = cross(cross(v1, v2), v1)。
由于我们假设这两条线相交,它们位于同一个平面上。通过将v1和v2进行叉乘得到的向量垂直于该平面。再次与v1进行叉乘将v3放回平面上,但同时也垂直于v1。因此,这个三维问题可以作为一个二维问题来处理,从而得到t的表达式。
有了线线相交问题的解决方案,线段相交问题现在只是一个简单的问题,只需要检查q是否同时位于两个线段上。只需要比较点积就可以判断q是否位于第一个线段上。对于第二个线段来说,检查起来更加容易,因为上述表达式总是将q放在第二条线上,也就是说,我们只需要检查t的值即可。
除了Bob的回答:
在测试中,我发现所写的intersection()函数解决了原问题的一半,原问题是要找到两个三维线段的交点算法。
假设这些线在同一平面内,则此问题有5种可能结果:
线段平行,因此它们不相交,或者
线段不平行,它们所在的无限长线相交,但交点不在任何一个线段的范围内,或者
线段相交,且交点在线段a的范围内而不在线段b的范围内,或者
线段相交,且交点在线段b的范围内而不在线段a的范围内,或者
线段相交,且交点在两个线段的范围内。
Bob的intersection()函数在线段相交且交点在线段a的范围内时返回true,但如果线段相交且交点仅在线段b的范围内,则返回false。
但是,如果您两次调用intersect(),首先使用线a然后是b,然后第二次使用线b和a(交换第一和第二个参数),那么如果两次调用都返回true,则相交点包含在两条线段内(情况5)。如果两次调用都返回false,则两条线段都不包含相交点(情况2)。如果只有一个调用返回true,则作为该调用的第一个参数传递的线段包含交点(情况3或4)。
此外,如果从norm2(cross(da,db))的调用返回值等于0.0,则表示线段平行(情况1)。
我在测试中注意到的另一件事是,对于通常使用代码实现的固定精度浮点数,dot(dc,cross(da,db))返回0.0非常不寻常,因此当其不是这种情况时返回false可能不是您想要的。您可能希望引入一个阈值,在该阈值以下,代码继续执行而不是返回false。这表示线段在3D中是斜的,但根据您的应用程序,您可能希望容忍一小部分偏差。
我注意到Bill代码中的最后一件事是:
ip = a.first + da * Coord(s,s,s);
那个 da * Coord(s,s,s) 看起来像是矢量乘法。当我用 da * s 的标量倍数替换它时,我发现它可以正常工作。
但无论如何,非常感谢 Bob。他解决了难点。
我找到了答案!
在上面的答案中,我找到了以下公式:
公式1:var s = Vector3.Dot(Vector3.Cross(dc, db), Vector3.Cross(da, db)) / Norm2(Vector3.Cross(da, db));
公式2: var t = Vector3.Dot(Vector3.Cross(dc, da), Vector3.Cross(da, db)) / Norm2(Vector3.Cross(da, db));
然后我修改了第三个方程:
公式3:
if ((s >= 0 && s <= 1) && (k >= 0 && k <= 1))
{
Vector3 res = new Vector3(this.A.x + da.x * s, this.A.y + da.y * s, this.A.z + da.z * s);
}
在保持方程式1和方程式2不变的同时,我创建了以下方程式:
MyEq#1: Vector3f p0 = da.mul(s).add(A<vector>);
MyEq#2: Vector3f p1 = db.mul(t).add(C<vector>);
然后我猜测创建了这三个方程式:
MyEq#3: Vector3f p0z = projUV(da, p0).add(A<vector>);
MyEq#4: Vector3f p1z = projUV(db, p1).add(C<vector>);
最后,通过计算projUV(1, 2)的两个大小之差,可以得到0和0.001f之间的误差边界,以确定两条线是否相交。
MyEq#5: var m = p0z.magnitude() - p1z.magnitude();
现在我要提醒你,这是用Java完成的。这个解释还没有符合Java的规范。只需要从上面的方程式开始工作即可。(提示:先不要转换到世界空间,这样UV方程的两个投影将正好落在您想要的地方)。
在我的程序中,这些方程是视觉上正确的。
2
原文链接
- 相关问题
- 3 圆与两条线段的交点没有检测到所有交点
- 8 连接两条线段
- 41 求两条直线的交点算法?
- 5 寻找线段-矩形交点
- 12 线段圆形交点
- 515 如何检测两条线段的交点?
- 4 1D中两条线段之间最短距离的高效算法
- 5 寻找两条直线的交点
- 5 两条平行线段的交点
- 3 两条线段的交点或重叠部分
z平面上。如果你将它们投影到 xy 平面上,那么它们会看起来相交,尽管它们实际上并没有相交。 - Graviton