我正在解决一个问题，它可以简化为以下的图优化问题。
给定一组有颜色的节点。它们都没有连接，即在图中没有边。
需要在这些节点之间插入边。
每个节点最多只能有4条边。
一张表格提供了从边缘获得利润的规则。
例如，
将红色节点与红色节点连接的边缘：利润为10。
将红色节点与蓝色节点连接的边缘：利润为20。
总节点数约为100个。
颜色总数通常在20到30种左右，但可能高达50种。对应的利润（边缘）表将是一个很长的列表，但它不会列出所有可能的组合。未在表中指定利润的边缘被认为是零。
问题是优化连接（边缘），使得总利润最大化。
我想知道是否已经有人研究过这个问题，如果有，请提供任何有帮助的参考。谢谢。
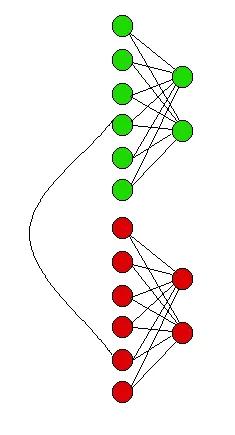
d个分裂节点的目的是每个分裂节点将连接到唯一的其他节点。不错。整个算法的复杂度是多少？ - justhalf这听起来很像0-1背包问题，其中最大值是通过将物品放入背包或不放入背包来计算的。以下是一个例子：
def knapsack(numItems, capacity, sizes, values):
# if no more items left to put in knapsack or knapsack is full
if (numItems == 0 or capacity == 0):
return 0
# if can't fit item into knapsack, try the next item
if (sizes[numItems-1] > capacity):
knapsack(numItems-1, capacity, sizes, values)
# find the max of including or not including item in knapsack
return max(
values[values-1] + knapsack(numItems-1,capacity - weights[numitems-1], sizes, values),
knapsack(numItems-1, capacity, sizes, values))
当一个节点连接或未连接时，您希望获得最大值。当节点连接时，结果取决于节点的颜色。代码可能如下所示：
def ConnectNodes(numItems, capacity, sizes, values, nodeColor):
# if no more items left to connect or capacity is full
if (numItems == 0 or capacity == 0):
return 0
# if can't fit item into knapsack, try the next item
if (sizes[numItems-1] > capacity):
ConnectNodes(numItems-1, capacity, sizes, values, nodeColor)
# find the max of connecting or not connecting node
return max(
RulesForProfit(numItems-1, nodeColor) + ConnectNodes(numItems-1,capacity - weights[numitems-1], sizes, values, nodeColor),
ConnectNodes(numItems-1, capacity, sizes, values, nodeColor))
然后在G上使用匹配算法（Blossom算法）。将这些边添加到O中。
使用输入G'=(V,E\O)再次重复该算法。再次将这些边添加到O中。
再次重复两次。返回O。
运行时间：
根据维基百科，Blossom算法的运行时间为O(E*V^(1/2))。由于该算法被使用了4次，因此总运行时间也将是O(E*V^(1/2))。
您是否考虑过贪心算法？对于所有颜色及其相应的colorA->colorB值，如果对于每个有色边缘，您都这样做：
edge_color : sort_in_descending_order(edge_color_To_color_Prices)
example:
red: red->black 30
red->white 20
red->yellow 10
black: black->green 15
black->grey 10
迭代直到有足够的空间来添加新的边（每个节点最多4条），并选择最大可能的边值（将其标记为已访问，这将有助于您以后的工作）（我假设您只能将nodeA与nodeB连接一次）。根据您所说的，我们可以假设边不是有向的。在每个节点中，您必须存储那些被选择的值，因此当您迭代下一个已使用的边时，您必须意识到已选择的边（黑色节点必须意识到由红色->黑色30选择的红色节点）。
red: 1st edge: red->black 30 -> stores that in black node list as
[red,30]
2nd edge: ...........20 ->...
3rd edge: ...........10
4th edge: ...........5
---------------------------
5th edge: ...........4 (after update from black it will be 4th
edge)
black: 1st edge: black->white 50 > [red,30]
2nd edge: .............. 40
3rd edge: .............. 35
4th edge: .............. 34
---------------------------
5th edge .............. 30 (this is our red->black edge)
替换成 (黑色->白色 50)，然后转到红节点以使用下一个最大值更新它(因为我们刚刚通过黑色->白色 50 删除了红色->黑色 30 - 只有在按照最小值标准遵循黑色节点中的边数限制时才替换它 - 我们正在从黑色节点中移除/替换最低价格的边)
应该可以了