我需要帮助实现一个算法，该算法可以生成建筑平面图。我最近在阅读Kostas Terzidis教授的最新著作Permutation Design: Buildings, Texts and Contexts（2014）时偶然发现了这个算法。
背景
考虑一个被分成网格系统的场地（a）。另外，考虑一个要放置在场地限制范围内的空间列表（c），以及一个邻接矩阵来确定这些空间的放置条件和相邻关系（d）。
如何根据单位所在邻居的理想程度重新排序？
编辑
正如一些人注意到的那样，该算法基于某些空间（由单位组成）相邻的可能性。因此，对于每个随机放置在站点限制内的单位：
- 我们先检查它的直接邻居（上下左右） - 如果至少有2个邻居，则计算适应度分数。（=这2个或更多邻居的权重之和） - 最后，如果相邻概率高，就放置该单位。
大致而言，可以这样翻译：
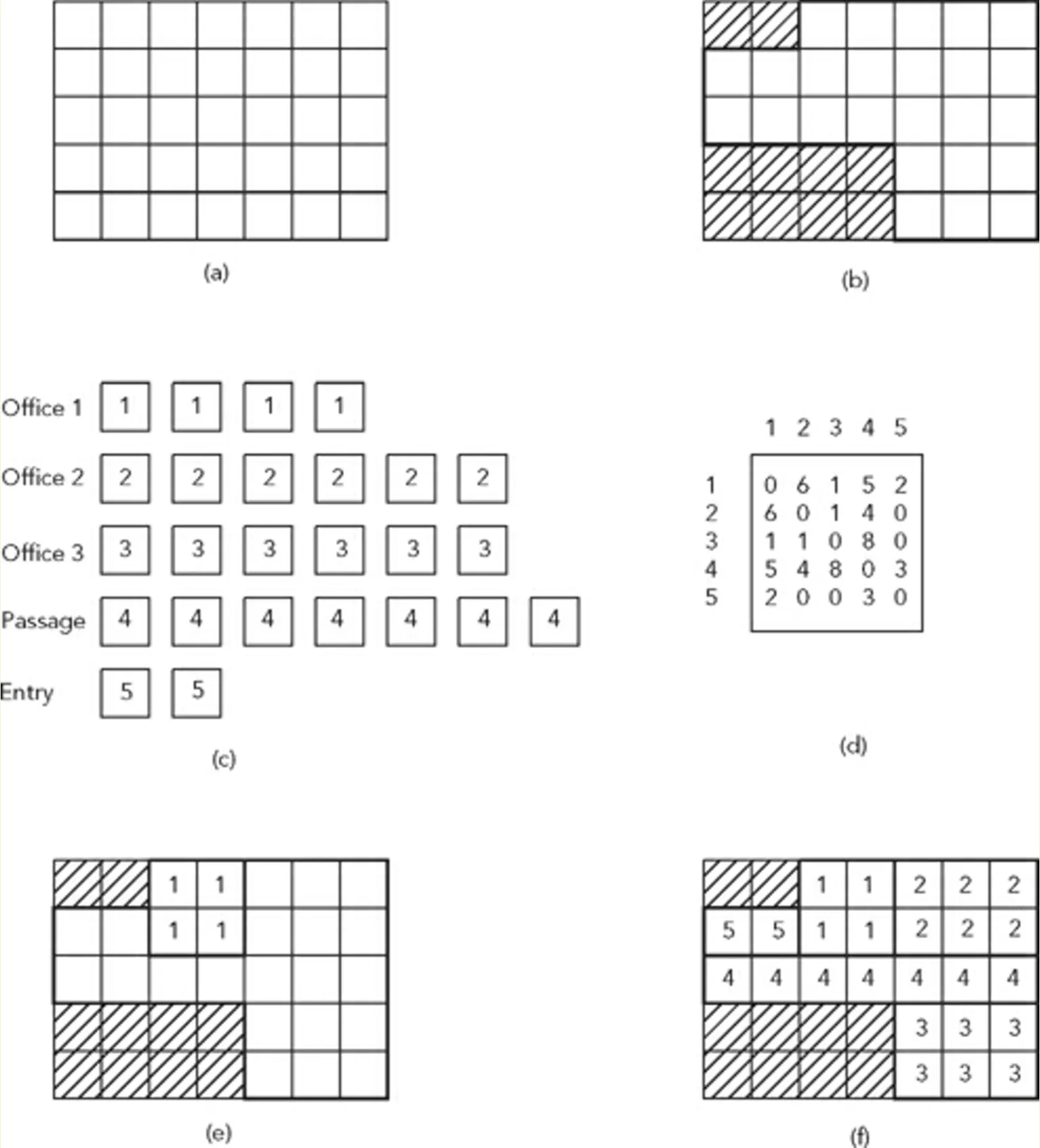
引用Terzidis教授的话：
“解决这个问题的一种方法是在网格中随机放置空格，直到所有空格都适合并且满足约束条件”
上图展示了这样一个问题和一个样本解决方案 (f)。
算法（在书中简要描述）
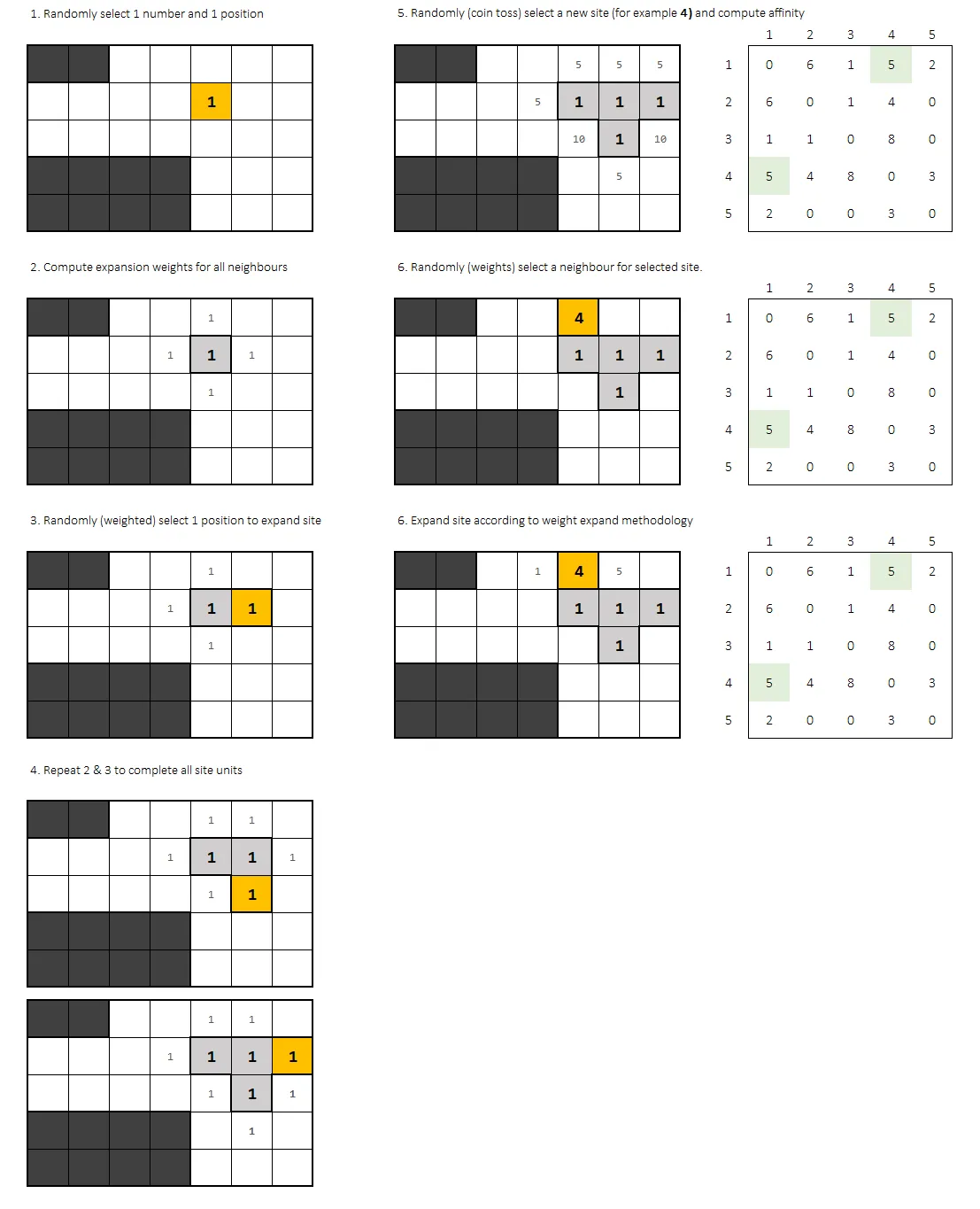
1/ “每个空格都与一个列表相关联，该列表包含根据期望邻域程度排序的所有其他空格。”
2/ “然后从列表中选择每个空格的每个单元，并将它们逐个随机放置在站点上，直到它们适合站点并且满足相邻条件。（如果失败，则重复此过程）”
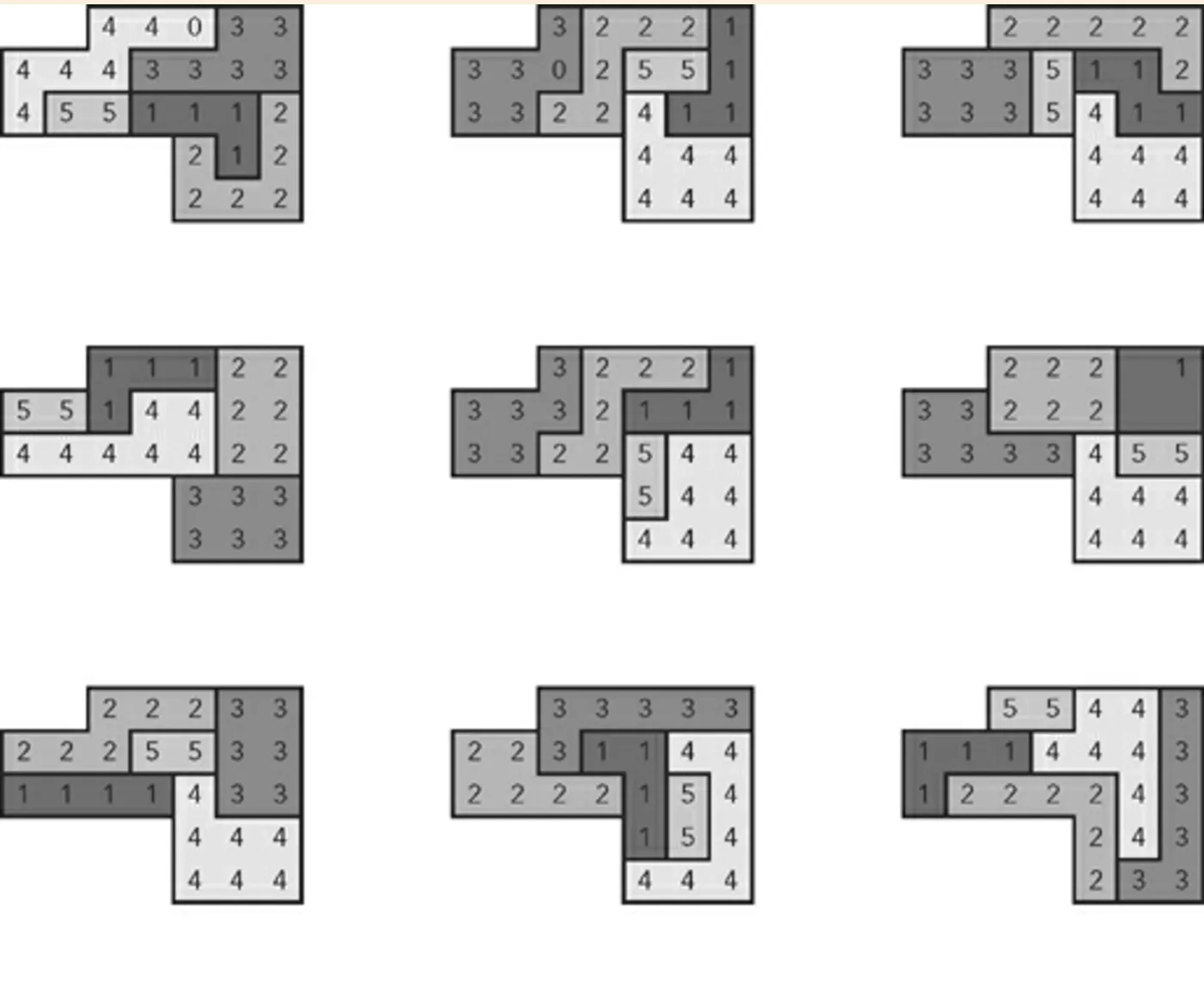
九个随机生成的计划示例：
我应该补充一下，作者后来解释说这个算法不依赖于蛮力技术。
问题
正如您所看到的，解释相对模糊，并且步骤2在编码方面相当不清晰。到目前为止，我只有“拼图的碎片”：
- 一个“站点”（选定整数列表）
- 邻接矩阵（嵌套列表）
- “空间”（字典列表）
对于每个单元：
- a function that returns its direct neighbors
- a list of its desirable neighbors with their indices in sorted order
a fitness score based on its actual neighbors
from random import shuffle n_col, n_row = 7, 5 to_skip = [0, 1, 21, 22, 23, 24, 28, 29, 30, 31] site = [i for i in range(n_col * n_row) if i not in to_skip] fitness, grid = [[None if i in to_skip else [] for i in range(n_col * n_row)] for e in range(2)] n = 2 k = (n_col * n_row) - len(to_skip) rsize = 50 #Adjacency matrix adm = [[0, 6, 1, 5, 2], [6, 0, 1, 4, 0], [1, 1, 0, 8, 0], [5, 4, 8, 0, 3], [2, 0, 0, 3, 0]] spaces = {"office1": [0 for i in range(4)], "office2": [1 for i in range(6)], "office3": [2 for i in range(6)], "passage": [3 for i in range(7)], "entry": [4 for i in range(2)]} def setup(): global grid size(600, 400, P2D) rectMode(CENTER) strokeWeight(1.4) #Shuffle the order for the random placing to come shuffle(site) #Place units randomly within the limits of the site i = -1 for space in spaces.items(): for unit in space[1]: i+=1 grid[site[i]] = unit #For each unit of each space... i = -1 for space in spaces.items(): for unit in space[1]: i+=1 #Get the indices of the its DESIRABLE neighbors in sorted order ada = adm[unit] sorted_indices = sorted(range(len(ada)), key = ada.__getitem__)[::-1] #Select indices with positive weight (exluding 0-weight indices) pindices = [e for e in sorted_indices if ada[e] > 0] #Stores its fitness score (sum of the weight of its REAL neighbors) fitness[site[i]] = sum([ada[n] for n in getNeighbors(i) if n in pindices]) print 'Fitness Score:', fitness def draw(): background(255) #Grid's background fill(170) noStroke() rect(width/2 - (rsize/2) , height/2 + rsize/2 + n_row , rsize*n_col, rsize*n_row) #Displaying site (grid cells of all selected units) + units placed randomly for i, e in enumerate(grid): if isinstance(e, list): pass elif e == None: pass else: fill(50 + (e * 50), 255 - (e * 80), 255 - (e * 50), 180) rect(width/2 - (rsize*n_col/2) + (i%n_col * rsize), height/2 + (rsize*n_row/2) + (n_row - ((k+len(to_skip))-(i+1))/n_col * rsize), rsize, rsize) fill(0) text(e+1, width/2 - (rsize*n_col/2) + (i%n_col * rsize), height/2 + (rsize*n_row/2) + (n_row - ((k+len(to_skip))-(i+1))/n_col * rsize)) def getNeighbors(i): neighbors = [] if site[i] > n_col and site[i] < len(grid) - n_col: if site[i]%n_col > 0 and site[i]%n_col < n_col - 1: if grid[site[i]-1] != None: neighbors.append(grid[site[i]-1]) if grid[site[i]+1] != None: neighbors.append(grid[site[i]+1]) if grid[site[i]-n_col] != None: neighbors.append(grid[site[i]-n_col]) if grid[site[i]+n_col] != None: neighbors.append(grid[site[i]+n_col]) if site[i] <= n_col: if site[i]%n_col > 0 and site[i]%n_col < n_col - 1: if grid[site[i]-1] != None: neighbors.append(grid[site[i]-1]) if grid[site[i]+1] != None: neighbors.append(grid[site[i]+1]) if grid[site[i]+n_col] != None: neighbors.append(grid[site[i]+n_col]) if site[i]%n_col == 0: if grid[site[i]+1] != None: neighbors.append(grid[site[i]+1]) if grid[site[i]+n_col] != None: neighbors.append(grid[site[i]+n_col]) if site[i] == n_col-1: if grid[site[i]-1] != None: neighbors.append(grid[site[i]-1]) if grid[site[i]+n_col] != None: neighbors.append(grid[site[i]+n_col]) if site[i] >= len(grid) - n_col: if site[i]%n_col > 0 and site[i]%n_col < n_col - 1: if grid[site[i]-1] != None: neighbors.append(grid[site[i]-1]) if grid[site[i]+1] != None: neighbors.append(grid[site[i]+1]) if grid[site[i]-n_col] != None: neighbors.append(grid[site[i]-n_col]) if site[i]%n_col == 0: if grid[site[i]+1] != None: neighbors.append(grid[site[i]+1]) if grid[site[i]-n_col] != None: neighbors.append(grid[site[i]-n_col]) if site[i]%n_col == n_col-1: if grid[site[i]-1] != None: neighbors.append(grid[site[i]-1]) if grid[site[i]-n_col] != None: neighbors.append(grid[site[i]-n_col]) if site[i]%n_col == 0: if site[i] > n_col and site[i] < len(grid) - n_col: if grid[site[i]+1] != None: neighbors.append(grid[site[i]+1]) if grid[site[i]+n_col] != None: neighbors.append(grid[site[i]+n_col]) if grid[site[i]-n_col] != None: neighbors.append(grid[site[i]-n_col]) if site[i]%n_col == n_col - 1: if site[i] > n_col and site[i] < len(grid) - n_col: if grid[site[i]-1] != None: neighbors.append(grid[site[i]-1]) if grid[site[i]+n_col] != None: neighbors.append(grid[site[i]+n_col]) if grid[site[i]-n_col] != None: neighbors.append(grid[site[i]-n_col]) return neighbors
如何根据单位所在邻居的理想程度重新排序？
编辑
正如一些人注意到的那样，该算法基于某些空间（由单位组成）相邻的可能性。因此，对于每个随机放置在站点限制内的单位：
- 我们先检查它的直接邻居（上下左右） - 如果至少有2个邻居，则计算适应度分数。（=这2个或更多邻居的权重之和） - 最后，如果相邻概率高，就放置该单位。
大致而言，可以这样翻译：
i = -1
for space in spaces.items():
for unit in space[1]:
i+=1
#Get the indices of the its DESIRABLE neighbors (from the adjacency matrix 'adm') in sorted order
weights = adm[unit]
sorted_indices = sorted(range(len(weights)), key = weights.__getitem__)[::-1]
#Select indices with positive weight (exluding 0-weight indices)
pindices = [e for e in sorted_indices if weights[e] > 0]
#If random grid cell is empty
if not grid[site[i]]:
#List of neighbors
neighbors = [n for n in getNeighbors(i) if isinstance(n, int)]
#If no neighbors -> place unit
if len(neighbors) == 0:
grid[site[i]] = unit
#If at least 1 of the neighbors == unit: -> place unit (facilitate grouping)
if len(neighbors) > 0 and unit in neighbors:
grid[site[i]] = unit
#If 2 or 3 neighbors, compute fitness score and place unit if probability is high
if len(neighbors) >= 2 and len(neighbors) < 4:
fscore = sum([weights[n] for n in neighbors if n in pindices]) #cumulative weight of its ACTUAL neighbors
count = [1 for t in range(10) if random(sum(weights)) < fscore] #add 1 if fscore higher than a number taken at random between 0 and the cumulative weight of its DESIRABLE neighbors
if len(count) > 5:
grid[site[i]] = unit
#If 4 neighbors and high probability, 1 of them must belong to the same space
if len(neighbors) > 3:
fscore = sum([weights[n] for n in neighbors if n in pindices]) #cumulative weight of its ACTUAL neighbors
count = [1 for t in range(10) if random(sum(weights)) < fscore] #add 1 if fscore higher than a number taken at random between 0 and the cumulative weight of its DESIRABLE neighbors
if len(count) > 5 and unit in neighbors:
grid[site[i]] = unit
#if random grid cell not empty -> pass
else: pass
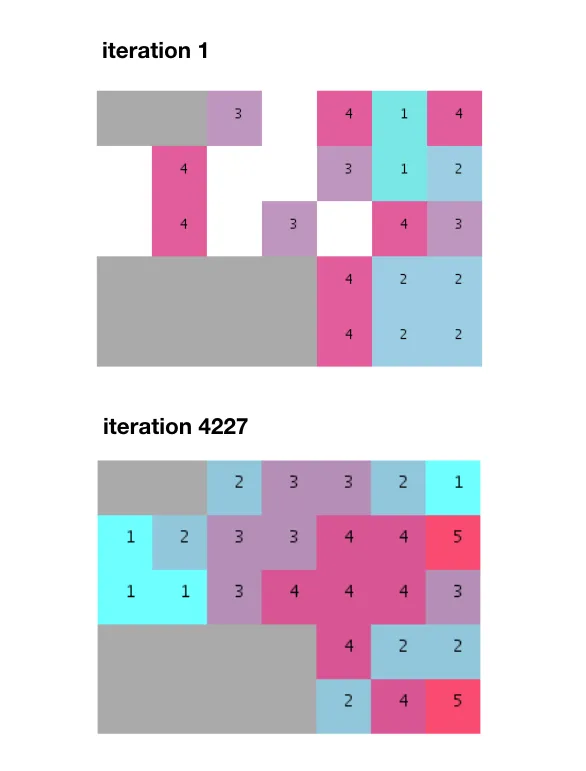
考虑到很大一部分单位不会在第一次运行时放置（因为邻接概率低），我们需要一遍又一遍地迭代，直到找到一个随机分布，其中所有单位都可以适应。
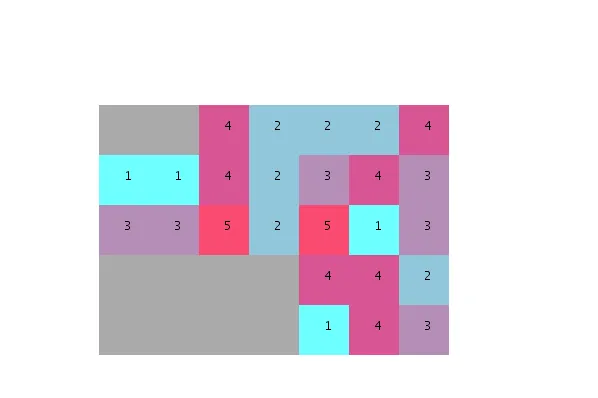
经过数千次迭代，找到了一个适合的拟合，并满足所有相邻要求。
然而，请注意此算法产生了分离的组，而不是像提供的示例中那样非分割和均匀的堆栈。我还应该补充一点，近5000次迭代比Terzidis先生在他的书中提到的274次迭代多得多。
问题：
- 我使用这种算法的方式有问题吗？
- 如果没有，那么我缺少什么隐含条件？
