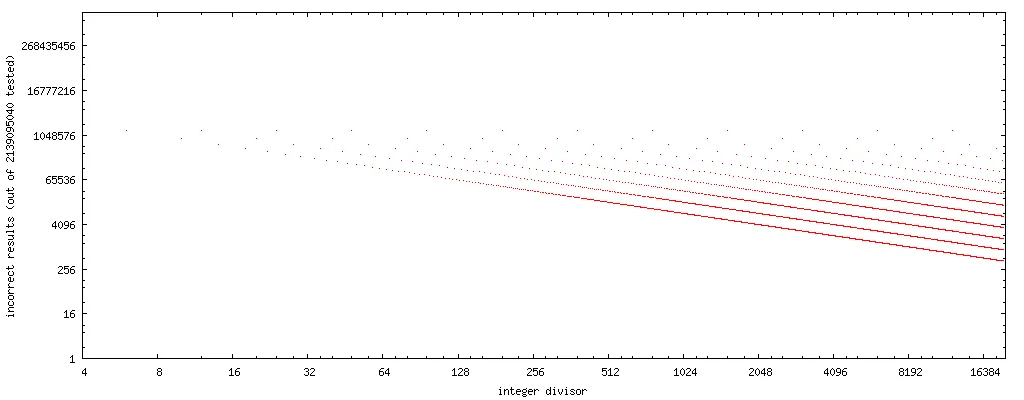
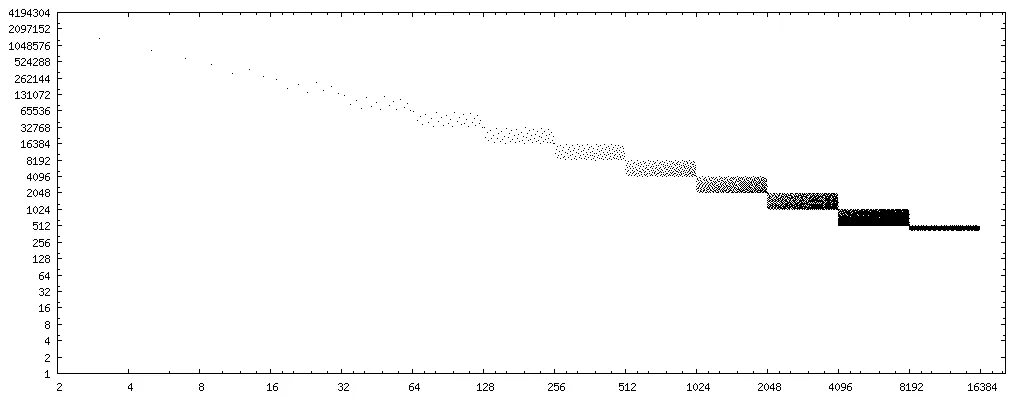
最近有一个问题,关于编译器是否允许用浮点乘法代替浮点除法,这启发了我提出这个问题。
在严格要求下,代码转换后的结果应该与实际除法操作的位相同,对于二进制IEEE-754算术,可以看出这对于2的幂次方除数是可能的。只要除数的倒数是可表示的,乘以除数的倒数就可以得到与除法相同的结果。例如,乘以0.5可以取代除以2.0。
然后我们想知道,在允许任何短的指令序列以更快的速度运行但提供位相同结果的情况下,对于其他除数,这种替换是否有效。特别是在纯乘法之外,还允许融合乘加运算。在评论中,我指出了以下相关论文:
Nicolas Brisebarre、Jean-Michel Muller和Saurabh Kumar Raina。已知除数时加速正确舍入的浮点除法。IEEE计算机学报,第53卷,第8期,2004年8月,pp. 1069-1072。
这篇论文提倡的技术是预先计算除数y的倒数作为标准化的头尾对zh:zl,方法如下:zh = 1 / y,zl = fma(-y, zh, 1) / y。然后,除法q = x / y被计算为q = fma(zh,x,zl * x)。该论文导出了除数y必须满足的各种条件,以便使此算法起作用。显而易见的是,当头和尾的符号不同时,此算法会遇到无穷大和零的问题。更重要的是,当被除数x的值非常小时,商的尾数zl * x的计算将受到下溢的影响,从而无法得出正确的结果。该论文还简单提到了一种替代的基于FMA的除法算法,由IBM的Peter Markstein开创。相关参考文献为:
P. W. Markstein. 计算IBM RISC System/6000处理器上的基本函数。 IBM研究与开发杂志,第34卷,第1期,1990年1月,111-119页。
在Markstein的算法中,首先计算倒数rc,然后形成初始商q = x * rc。然后,使用FMA精确地计算除法的余数r = fma (-y,q,x),最终计算出更准确的商q = fma (r,rc,q)。
该算法对于x为零或无穷大也存在问题(可以通过适当条件执行轻松解决),但是使用IEEE-754单精度float数据进行全面测试表明,它在许多除数y中为所有可能的被除数x提供正确的商,其中包括许多小整数。这段C代码实现了它:
/* precompute reciprocal */
rc = 1.0f / y;
/* compute quotient q=x/y */
q = x * rc;
if ((x != 0) && (!isinf(x))) {
r = fmaf (-y, q, x);
q = fmaf (r, rc, q);
}
在大多数处理器结构中,这应该转化为一系列无分支的指令,使用谓词、条件移动或选择类型指令。举个具体例子:对于除以
3.0f,CUDA 7.5的nvcc编译器为Kepler级别的GPU生成以下机器代码: LDG.E R5, [R2]; // load x
FSETP.NEU.AND P0, PT, |R5|, +INF , PT; // pred0 = fabsf(x) != INF
FMUL32I R2, R5, 0.3333333432674408; // q = x * (1.0f/3.0f)
FSETP.NEU.AND P0, PT, R5, RZ, P0; // pred0 = (x != 0.0f) && (fabsf(x) != INF)
FMA R5, R2, -3, R5; // r = fmaf (q, -3.0f, x);
MOV R4, R2 // q
@P0 FFMA R4, R5, c[0x2][0x0], R2; // if (pred0) q = fmaf (r, (1.0f/3.0f), q)
ST.E [R6], R4; // store q
为了进行我的实验,我编写了下面展示的小型C语言测试程序,它按照递增顺序遍历整数除数,并针对每个除数详尽地测试上述代码序列与正确除法的匹配性。它会打印出通过了这个详尽测试的除数列表。部分输出如下:
PASS: 1, 2, 3, 4, 5, 7, 8, 9, 11, 13, 15, 16, 17, 19, 21, 23, 25, 27, 29, 31, 32, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 64, 65, 67, 69,
作为一种优化方式,将替换算法加入编译器中是不可行的,因为无法列出适用于上述代码转换的除数白名单。该程序迄今为止的输出(每分钟约一个结果)表明,在奇整数或2的幂次方的除数y对x进行所有可能的编码时,快速代码的工作正确。当然,这只是一些例证,而不是证明。 有哪些数学条件可以事先确定将除法转换为上述代码序列是否安全? 答案可以假设所有浮点运算都在“四舍五入到最近的偶数”默认舍入模式下执行。
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
int main (void)
{
float r, q, x, y, rc;
volatile union {
float f;
unsigned int i;
} arg, res, ref;
int err;
y = 1.0f;
printf ("PASS: ");
while (1) {
/* precompute reciprocal */
rc = 1.0f / y;
arg.i = 0x80000000;
err = 0;
do {
/* do the division, fast */
x = arg.f;
q = x * rc;
if ((x != 0) && (!isinf(x))) {
r = fmaf (-y, q, x);
q = fmaf (r, rc, q);
}
res.f = q;
/* compute the reference, slowly */
ref.f = x / y;
if (res.i != ref.i) {
err = 1;
break;
}
arg.i--;
} while (arg.i != 0x80000000);
if (!err) printf ("%g, ", y);
y += 1.0f;
}
return EXIT_SUCCESS;
}