运算符和操作数的排列组合算法

Question

运算符和操作数的排列组合算法

12

我在一个面试网站上看到了这个问题 - 我们得到 4 个数字，比如 n1、n2、n3、n4。我们可以以任何顺序放置它们，并且我们可以在它们之间使用数学运算符 +、-、*、/，以便最终结果为 24。编写一个算法-它将取 4 个数字并返回 false 或 true，以指示是否可以使用任何组合获得最终结果 24。相同的操作符可以多次使用。

其中一种方法是：

1. 对运算符进行排列 2. 对操作数进行排列 3. 将第二步中的每个排列应用于第一步中的每个排列。

此解决方案将是暴力的，并不是最优的解决方案。我认为可能有一种更好的解决方案，使用二叉搜索树。

- Tushar Gupta

1个回答

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- Dr. belisarius · Accepted Answer

使用逆波兰表示法（RPN）

有关逆波兰表示法的介绍，请参见此处。

问题规模

我们需要构建一个由四个数字组成的列表，这意味着有三个运算符。
这些数字和运算符将被推入或执行到栈中。

让我们把执行列表称为 {a1 a2 a3 a4 a5 a6 a7}。

{a1 a2} 应该是数字，因为栈上没有一元操作。

{a7} 应该是一个运算符，以完成操作。

对于 {a3, a4, a5, a6}，我们有几个选项，但必须至少有两个数字在栈中才能进行操作。所以可能的组合是：（N=数字，O=运算符）

{N N O O}、{N O N O}、{O N O N}、{O N N O} 和 {N O O N}。

组合 {O O N N} 是禁止的，因为第二个 O 时栈为空。

所以我们有：

      | {N N O O} |  
      | {N O N O} |  
{N N} | {O N O N} | {O}  
      | {O N N O} |  
      | {N O O N} |

现在我们将计算可能的排列方式。当然，我们会过度计数，因为可交换的运算符（加号和乘号）可能会将排列树分成两半，但问题足够小，不必担心这个问题。（在序列是{OO}的情况下，我们也会过度计数。但我们只需继续...）

我们必须在四个数字中选择2个数字作为第一段，这是12个可能的排列方式。

对于中间段，剩下的两个数字只能进行排列，即因子为2。

但我们有另一个因子5来计算中间段的五个替代方案。

对于三个运算符，由于它们可以重复，因此我们有一个因子4^3=64 因此，问题的规模是粗体数字的乘积：12 2 5 64 = 7680。不需要优化，我们可以通过蛮力继续前进。

问题的其余部分是构建7680个排列和RPN评估器。两个相对容易的任务。

以下是递归RPN评估器的代码。我选择用函数式语言（Mathematica）编写，以简化操作符解析。

rpn[listipt_, stackipt_: {}] := 
  Module[{list=listipt,stack=stackipt}, (*recursive rpn evaluator*)

    If[list == {}, Return[stack[[1]]]];        (*end*)
    If[NumberQ[list[[1]]],                     (*if numeric*)
     Return@rpn[Rest[list], PrependTo[stack,list[[1]]]];  (*push nbr and recurse*)
    ,
     (stack[[2]]=list[[1]][stack[[2]], stack[[1]]];       (*if not, operate*)
      Return@rpn[Rest[list], Rest[stack]];);              (*and recurse*)
   ];
];

使用示例

rpn[{1, 1, 1, Plus, Plus}]
3

rpn[{2, 2, 2, Plus, Plus}]
6

rpn[{2, 3, 4, Plus, Times}]  (* (4+3)*7 *)
14

rpn[{2, 3, 4, Plus, Divide}]  (* (2+3)/4 *)
2/7

稍后我会发布元组生成器并展示它们有7680个，以及一些有趣的关于操作可能结果分布的结果（事实上对于{1,2,3,4}集合，你只能得到230个不同的结果！）。

编辑：元组构建

首先我们明确构建中间段的可能性。

t1 = {{n3, n4, o1, o2}, 
      {n3, o1, n4, o2}, 
      {o1, n3, o2, n4}, 
      {o1, n3, n4, o2}, 
      {n3, o1, o2, n4}};

现在我们在{n1，n2}和最后一个运算符之前添加两个变量。

t2 = Join[Map[Join[{n1, n2}, #, {o3}] &, t1], 
          Map[Join[{n2, n1}, #, {o3}] &, t1]] ( bahh ... don't mind the code*)

导致我们有10种不同的配置。

alt text

现在我们需要使用所有可能的数字和运算符的排列组合来填充所有这些配置。

我们首先将所有数字排列构建为元组的赋值规则。

 repListNumbers = (*construct all number permutations*)
    Table[{n1 -> #[[1]], n2 -> #[[2]], n3 -> #[[3]], n4 -> #[[4]]} &[i], 
         {i, Permutations[{1, 2, 3, 4}]}];

这些小东西的形式为

  {n1 -> 1, n2 -> 2, n3 -> 3, n4 -> 4}

我们可以使用它们来替换元组中的值。例如：

  {n1,n2,n3,o1,o2,n4,o3} /. {n1 -> 1, n2 -> 2, n3 -> 3, n4 -> 4}

结果为

  {1,2,3,o1,o2,4,o3}

当然，我们可能已经将替换规则构建为函数，以便随意更改数字集合。我们现在也可以通过类似的方式处理运算符。

repListOps =      (*Construct all possible 3 element tuples*)
  Table[{o1 -> #[[1]], o2 -> #[[2]], o3 -> #[[3]]} &[i], 
      {i, Tuples[{Plus, Times, Divide, Subtract}, 3]}];

所以，我们得到了一组诸如

的东西

 {o1->Plus, o2->Plus, o3->Divide}

现在我们将元组和所有替换规则合并到一个大列表中：

t3 = Flatten[t2 /. repListNumbers /. repListOps, 2];

这导致了15360个不同的计算结果。但我们知道它们被重复计算了两次，因此现在我们去掉重复的元素：

t3 =Union[t3]

我們預期得到7680個元素。

仍然存在一些重複計算，因為{2,3,Times} = {3,2,Times} = 6，但對於我們目前的目的來說這是可以的。

評估結果

現在我們有了RPN求值器和所有那些元組，我們想知道是否可能存在某個特定的最終結果。

我們只需問該數字是否包含在結果集中即可：

In[252]:= MemberQ[rpn /@ t3, 24]
Out[252]= True

In[253]:= MemberQ[rpn /@ t3, 38]
Out[253]= False

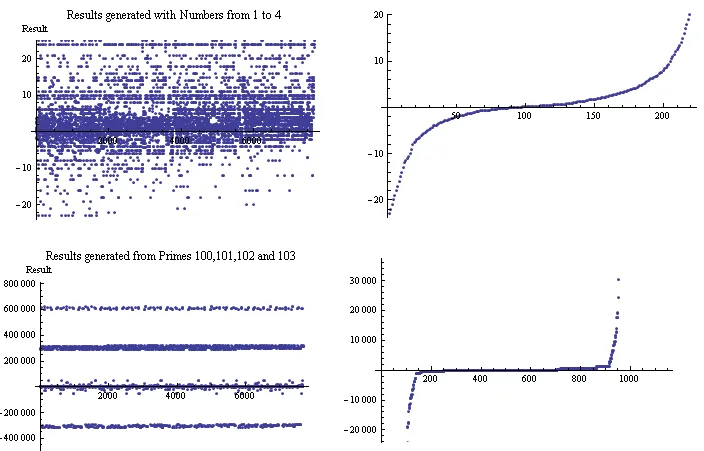
实际上，结果集的范围是：

In[254]:= Max[rpn /@ t3]
Out[254]= Max[36, ComplexInfinity]

In[255]:= Min[rpn /@ t3]
Out[255]= Min[-23, ComplexInfinity]

无穷大的结果是因为我没有考虑除以零的情况，所以它们存在于集合内部。数字区间为[-23，36]。

如果您想知道有多少结果等于24，只需计数即可。

      In[259]:= Length@Select[t3, rpn[#] == 24 &]
      Out[259]= 484

当然，它们中的许多都是由于“加”和“乘”的可交换性质而产生的琐碎排列，但并非所有情况都是如此：

   {1, 2, Plus, 3, Plus, 4, Times}      -> ((1+2)+3)*4  = 24
   {2, 1, 4, 3, Times, Divide, Divide}  ->  2/(1/(4*3)) = 24

没有使用"Subtract"操作符的序列可以得到24！

    In[260]:= MemberQ[Flatten@Select[t3, rpn[#] == 24 &], Subtract]
    Out[260]= False

结果频谱样本

alt text