渐近紧密界限（asymptotic tight bound）对于二次函数

Question

在CLRS（由Cormen、Leiserson、Rivest和Stein编写的算法导论）中，对于一个函数

f(n) = an² + bn + c

他们说

假设我们取常数c₁ = a/4，c₂ = 7a/4和n₀ = 2·max(|b|/a, √(|c|/a))。 那么对于所有n ≥ n₀，有0 ≤ c₁n² ≤ an² + bn + c ≤ c₂n²。 因此，f(n)是Θ(n²)。 但他们没有说明这些常数的值是如何得出的？ 我试图证明它，但失败了。 请告诉我这些常数是如何得出的？

- Happy Mittal

Answer 1

这些常数并没有什么特别的（除了它们与特定的 n 值上满足 f 的theta-ness这一事实）。没有神奇之处。如果你能找到其他正常数，使得该关系成立同样有效（事实上，c1可以是任何0<k<1的ka）。虽然既然它们在那里，让我们分析一下c1：

我们需要它满足以下不等式：

c1*n^2 <= an^2 + bn + c

让我们来看一下它们的值：c1 = a/4。对于什么样的n我们可以保证这个不等式成立？我们可以解决：

a/4*n^2 <= an^2 + bn + c
<==> 0 <= 3a/4*n^2 + bn + c

二次方程的解为(-b +- sqrt(b^2-3ac)) / (3a/2)，其中只有正数解是有意义的，因为我们有一个正导数的多项式，所以我们需要n > 2 * (sqrt(b^2-3ac) - b) / 3a，这在假设b^2 >= 3ac的情况下是很好定义的（如果不是，则二次方程是正定的，这更好，因为它在任何地方都大于等于0，并且该不等式对所有n都成立）。我应该指出，这是一个有效的解，尽管我们将进行更多的工作，直到达到书中的表示形式。

我们可以将分析分为两种情况。首先，让我们假设|b|/a >= sqrt(|c|/a)。因此，我们可以通过4b^2将sqrt(...)内部的上限绑定，并要求n > 2/3 * [sqrt(4b^2)-b]/a，这可以被上界2|b|/a所限制。

第二种情况，让我们假设|b|/a < sqrt(|c|/a)。因此，我们可以通过4a|c|将sqrt(...)内部的上限绑定，并要求n > 2/3 * [sqrt(4a|c|)-b]/a，这可以被上界2sqrt(|c|/a)所限制。

因此，在每种情况下，我们可以看到当我们取max(|b|/a, sqrt(|c|/a))时，我们的不等式在n > 2 * max时成立。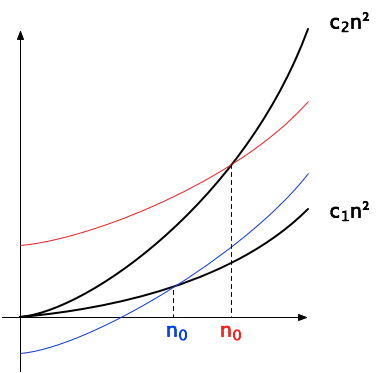

类似地，对于c2也是如此。

- davin

---

如果 b^2 >= 3ac ... 因为它 > 0 - chakmeshma

Answer 2

这个方法的思路是（对于足够大的n），将所需函数夹在两个“纯”增长函数之间（这些函数只有单个比例常数）。在这张图中，两个二次函数（绘制为红色和蓝色）被夹在两个纯增长函数（绘制为黑色）之间，每种情况下最小可能值的n₀都已指出。 因此，一旦您选择了c₁和c₂的值，就可以通过将您的函数与两个纯增长函数相交并取最右侧的交点来找到n₀的值。

但是，您不需要关心获取n₀的最小可能值 - 我们在这里进行渐近分析，因此任何足够大的值都可以 - 因此，您可以使用近似值来得到其上限。

请参见davin的答案，了解如何将n₀的上限转换为CLRS中给出的形式。

- Gareth Rees

---

你从哪里得到了15？1-1/4=3/4!=15。看起来你不小心把a/4平方了。 - davin

哦，我明白了。那不是我犯的唯一愚蠢错误。现在我看到你已经做对了，所以我会参考你的答案。 - Gareth Rees

Answer 3

很容易 1.c1<=a + b/n + c/n^2 这里a>0，而b和c可以是正数或负数 现在我们必须选择n的值，使得上面方程式中RHS中的b/n+c/n^2从未超过a，否则它将变为负数，c1也将变为负数。但按照定义c1是一个正常数

所以，我们要确保 a>b/n+c/n^2

如果我们选择n=2*max(|b|/a, sqrt(|c|/a)) 我们将得到b/n+c/n^2的表达式，其值小于a/2+a/4。

因此，a+b/n+c/n^2的最大值为a+a/2+a/4，最小值为a-(a/2+a/4)，即c2和c1的值。

c1=a-a/2-a/4= a/4 c2=a+a/2+a/4= 7a/4

这个概念可以扩展到任何多项式的任何值..

干杯!!!

- Ravi Karki

Answer 4

c1和c2可以任意选择，只要满足0 < c1 < a和a < c2 < 无穷大。 然后根据这个计算出n0，以便对于所有n>=n0，不等式0 <= c1*n^2 <= an^2 + bn + c <= c2*n^2都成立。

- Henrik

---

那么为什么他们特别提到这些值呢？我的意思是，他们提供的这些值似乎并不是随意的。此外，他们如何计算n0？ - Happy Mittal

Answer 5

P(n) = an² + bn + c = an²( 1 + b / ( an ) + c / ( an² )) = an²( 1 ± ( | b | / a ) / n ± ( √( | c | / a ) / n )²
因此，如果我们以q = max( | b | / a, √( | c | / a ))为例，则
P(n) ≤ an²( 1 + ( q / n ) + ( q / n )² )，如果我们取n₀ = q，那么我们将得到第二个常数
c₂ = 3a，对于下限同理

- baz

---

| b | / a, √( | c | / a ) 这些值从哪里来的？ - piku_baba

Answer 6

为了证明任意多项式f(n)=a0+a1*n+a2*n^2+a3*n^3+...+am*n^m是theta(n^m)，只需要按照两个简单的步骤来进行。 步骤1：证明f(n)是bigOh(n^m) 步骤2：证明f(n)是bigOmega(n^m)

如果以上两个条件都成立，那么f(n)肯定是bigTheta(n^m)。

这是一个推广。当m=2时，你得到f(n)是bigTheta(n^2)。 简单吧.. 是不是？

- bilol