用C++找到一对椭圆的公切线的首选方法

Question

我希望用C++实现这个功能，我有两个想法：

1. 将椭圆对作为两个不同参数的参数方程来考虑，可以得到两个关于两个参数的方程。这一对方程是非线性的，其中包含余切、正弦和余弦的函数。Geant4是我主要使用的工具，但它只支持多项式。
2. 使用一个几何库来解决这个问题。我研究了Boost geometry，但文档不连贯（对我来说），似乎更适用于计算几何。也许我在要求Y时，本来只是要求X。

怎样才能解决这个问题呢？ 在Python中很容易，我甚至可以在睡觉时做到。任何见解都将不胜感激。自从我开始学习C++以来，选择使用的库就像是一场巨大的战斗。

- rooms

---

什么是一对椭圆的公切线？（可能有多个）添加一个示意图。您拥有哪些椭圆的解决方案约束（轴对齐或通用）？椭圆很棘手，许多几何问题我们不知道如何代数计算，而是使用数值、图形和近似方法（因为超越方程组）。请查看此处的示例方法，了解如何执行此操作：https://dev59.com/zOo6XIcBkEYKwwoYGwQZ - Spektre

Answer 1

我有几个建议。您可以尝试使用LibreCAD，它具有用于两个椭圆公切线的求解器，但我不了解API。该求解器解决四次方程，这是如果您天真地尝试找到两个椭圆的公切线所获得的结果。

如果您想自己编写代码：通过一些理论（“锥体范围”），您可以使用线性代数（即查找3x3矩阵的逆）以及解决二次和一个三次方程来完成您所需的内容。步骤如下：

您可以将任何锥体（例如椭圆）表示为矩阵方程的形式。

        [m00 m01 m02] [x]
[x,y,z] [m10 m11 m12] [y] = 0
        [m20 m21 m22] [z]

矩阵M对称，[x,y,z]是齐次坐标，可以将方程简写为X M X^T = 0，其中X^T是X的转置。请将z=1视为常数。

平面上的直线可以写成lx+my+nz=0的形式，因此具有“线坐标”(l,m,n)。

上述圆锥曲线的切线集可以用这种符号表示非常简单。设A是矩阵M的逆矩阵，则圆锥曲线的切线集为：

        [a00 a01 a02] (l)
(l,m,n) [a10 a11 a12] (m) = 0
        [a20 a21 a22] (n)

现在假设我们有第二个二次曲线，其矩阵为N，并且N具有逆矩阵B。一条公切线将满足上述方程和方程。

        [b00 b01 b02] (l)
(l,m,n) [b10 b11 b12] (m) = 0
        [b20 b21 b22] (n)

事实上，我们可以将后一个方程中的矩阵乘以t，它仍然成立：

          [b00 b01 b02] (l)
(l,m,n) t [b10 b11 b12] (m) = 0
          [b20 b21 b22] (n)

将第一个圆锥曲线的切线方程加到第二个圆锥曲线的上述方程中，我们得到矩阵方程 L (A + tB) L^T = 0。因此，任何两个圆锥曲线的公共切线都是每个在“范围” A + tB 中的圆锥曲线的公共切线。

现在来看一个大大简化问题的想法：我们可以在该范围内找到一些非常特殊的圆锥曲线，“退化”的圆锥曲线，它们只是一对点。由于公共切线必须通过所有圆锥曲线，所以它们必须通过这些退化的圆锥曲线。但是，很容易找到通过退化的圆锥曲线的直线，因为这样的圆锥曲线只是一对点！

通过解三次方程det(A + tB) = 0来找到退化圆锥曲线，其中det()是3x3矩阵的行列式。可以通过Cardano公式或其变形来解决这个三次方程，也可以进行数值求解。一旦找到使圆锥曲线退化的t的值，就可以将方程L (A + tB) L^T = 0分解为两个线性因子。每个线性因子xl + ym + zn = 0在齐次坐标[x,y,z]或笛卡尔坐标(x/z,y/z)中定义一个点。可以通过这种方式得到三对点（六个点）。通过某些点对的直线将给出四条最多的切线。

以下是一个简单的例子（其中两个椭圆的中心都在原点）：找到x^2+2y^2=3和x^2+14y^2=7的公切线。矩阵形式的圆锥曲线如下：

        [1 0  0] [x]               [1  0  0] [x]
[x,y,z] [0 2  0] [y] = 0,  [x,y,z] [0 14  0] [y] = 0
        [0 0 -3] [z]               [0  0 -7] [z]

切线由以下给出

        [6 0  0] (l)               [14 0  0] (l)
(l,m,n) [0 3  0] (m) = 0,  (l,m,n) [ 0 1  0] (m) = 0
        [0 0 -2] (n)               [ 0 0 -2] (n)

注意，我已经将逆矩阵乘以一个标量，只是为了使其条目成为整数而不是有理数。你不必这样做，但这会使手动计算更容易。将第二个矩阵乘以一个额外的标量 t 可得

        [6+14t 0    0   ] (l)
(l,m,n) [0     3+t  0   ] (m) = 0
        [0     0   -2-2t] (n)

当 (6+14t)(3+t)(-2-2t)=0 时，圆锥曲线是退化的，即当 t=-3/7, -3, -1 时。当 t=-3/7 时，我们得到

18/7 m^2 - 8/7 n^2 = 2/7 (9 m^2 - 4 n^2) = 2/7 (3m - 2n)(3m + 2n) = 0

这对应于具有齐次坐标[x，y，z] = [0,3，-2]和[0，3，2]的点，换句话说，具有笛卡尔坐标(0，-3/2)和(0，3/2)的点。

当t = -3时，我们得到-36l ^ 2 + 4n ^ 2 =（6l + 2n）（-6l + 2n）= 0，点[6,0,2]和[-6,0,2]或在笛卡尔坐标中(3,0)和(-3,0)。 最后，当t = 1时，我们得到-8l ^ 2 + 2m ^ 2 = 2（2l + m）（-2l + m）= 0对应于点[2,1,0]和[-2,1,0]，它们是无穷远点。

现在先避免无限远点，因为它们稍微难处理，我们通过以下点对获得四条线：

{(0,-3/2),(-3,0)}, {(0,-3/2),(3,0)}, {(0,3/2),(-3,0)}, {(0,3/2),(3,0)}

这给我们提供了两个椭圆的四条常见切线。

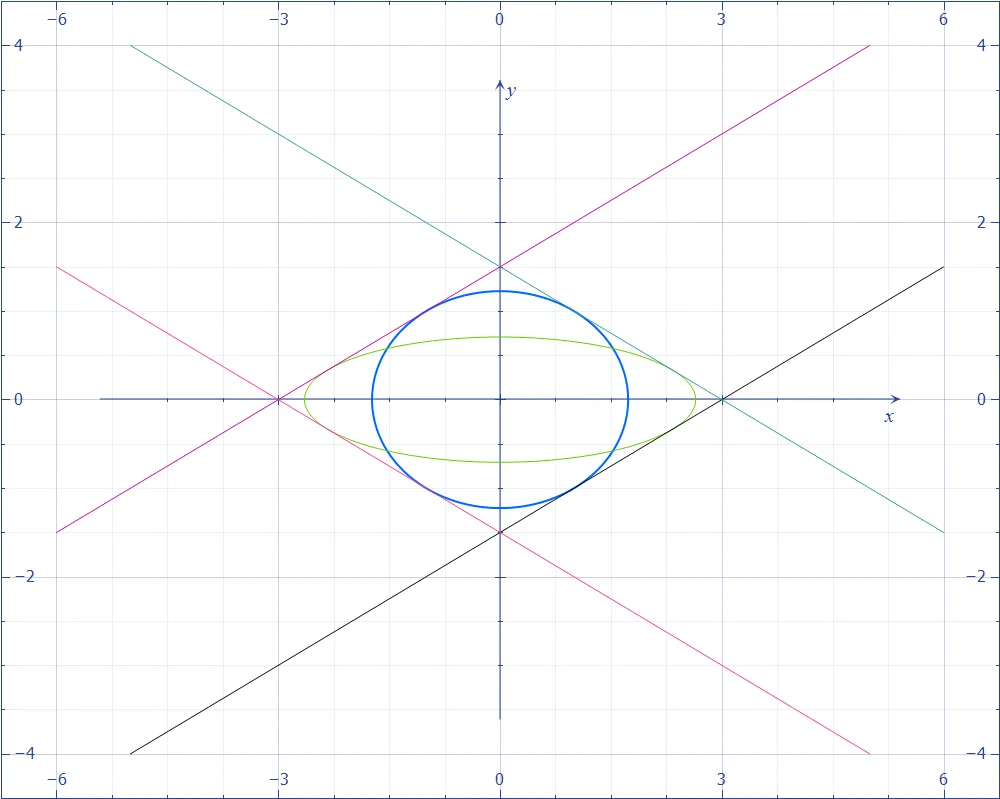
你可以从图片中看出，共切线也经过无穷远点[2,1,0]和[-2,1,0]，即平行线对具有斜率1/2和-1/2。

这不是很美吗？

- Edward Doolittle

---

我有一个关于倒数第二步的问题：一旦您找到使退化圆锥体的t的值，您可以将方程L（A + tB）L^T = 0因式分解为两个线性因子。这是什么意思？如果您觉得这很琐碎，对不起，我的线性代数还有点生疏。之后就是连接各个单独的点，其中最多有4个共同切线，对吗？感谢您，我喜欢此解决方案的优雅（当然，前提是我完全理解它！） - rooms

嗨，我再仔细想了一下，似乎你提供的示例中由det（A + Bt）= 0生成的圆锥曲线当然是退化的，但没有一个是点。两对是平行线，一对是相交线。我想我可能漏掉了什么。谢谢。 - rooms

方程式 L (A + tB) L^T = 0 是一个二次形式，涉及到项 l^2, m^2, n^2, lm, mn, nl。通常情况下（当二次形式的图形是非退化圆锥曲线时），该形式不能分解为两个线性因子。当形式退化（矩阵行列式为零）时，该形式可以分解。一种分解方法是使用二次公式：将 l 视为变量，m,n 视为常数。您关于连接点的想法是正确的；6个点给出15对，其中3对是无关的（来自相同t的点）。另外12个中的4个给出了公共切线。 - Edward Doolittle

@rooms：关于退化线圆锥如何定义点的问题：你正在思考退化点圆锥是一对直线。我们在这里讨论的是退化线圆锥，它们是一对点。情况是对偶的。这可能会令人困惑，因为人们似乎已经忘记了对偶、线圆锥和射影几何中的其他美妙思想。我甚至找不到一个综合性的参考资料，虽然我从谷歌图书中找到了一个旧书的例子。 - Edward Doolittle