如何确定一个点是否在一个二维三角形内?
7
这里是一个高效的Python实现:
def PointInsideTriangle2(pt,tri):
'''checks if point pt(2) is inside triangle tri(3x2). @Developer'''
a = 1/(-tri[1,1]*tri[2,0]+tri[0,1]*(-tri[1,0]+tri[2,0])+ \
tri[0,0]*(tri[1,1]-tri[2,1])+tri[1,0]*tri[2,1])
s = a*(tri[2,0]*tri[0,1]-tri[0,0]*tri[2,1]+(tri[2,1]-tri[0,1])*pt[0]+ \
(tri[0,0]-tri[2,0])*pt[1])
if s<0: return False
else: t = a*(tri[0,0]*tri[1,1]-tri[1,0]*tri[0,1]+(tri[0,1]-tri[1,1])*pt[0]+ \
(tri[1,0]-tri[0,0])*pt[1])
return ((t>0) and (1-s-t>0))
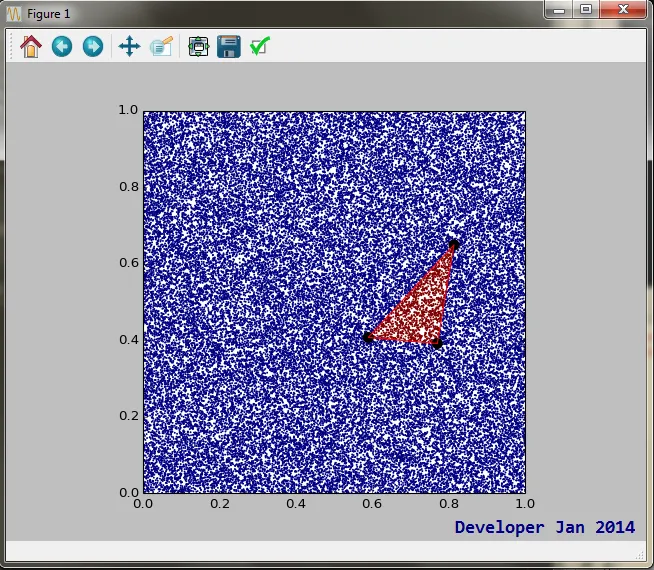
这是一个例子输出:
1
在3D中通过侧向量和面法向量的叉乘计算。
在2D中,只需交换组件并否定其中一个。
好处:
很多内容都已经预先计算,因此适用于同一三角形的多个点测试。
早期拒绝常见的更多外部点的情况。(如果点分布加权到一侧,还可以首先测试该侧。)
按照它们的纵坐标对三角形顶点进行排序。这最多需要三次比较。让Y0、Y1、Y2成为三个排序后的值。通过在它们之间画出三条水平线,您可以将平面分为两个半平面和两个平板。让Y成为查询点的纵坐标。
if Y < Y1
if Y <= Y0 -> the point lies in the upper half plane, outside the triangle; you are done
else Y > Y0 -> the point lies in the upper slab
else
if Y >= Y2 -> the point lies in the lower half plane, outside the triangle; you are done
else Y < Y2 -> the point lies in the lower slab
需要进行两次额外的比较成本。正如您所看到的,对于在“包围板块”之外的点,可以实现快速拒绝。
作为可选项,您可以提供一个关于横坐标的测试,以便在左边和右边进行快速拒绝(X <= X0' or X >= X2')。这将同时实现一个快速包围框测试,但您需要按照横坐标排序。
最终,您需要计算给定点相对于限定相关板块(上或下)的两侧三角形的符号。测试的形式为:
((X - Xi) * (Y - Yj) > (X - Xi) * (Y - Yj)) == ((X - Xi) * (Y - Yk) > (X - Xi) * (Y - Yk))
完整讨论i、j、k的组合(根据排序结果有六个)超出了本答案的范围,留给读者自己练习;为了提高效率,它们应该被硬编码。
如果你认为这个解决方案很复杂,请注意它主要涉及简单的比较(其中一些可以预先计算),加上6次减法和4次乘法(在边界框测试失败的情况下)。后者的成本难以打败,因为在最坏的情况下,您无法避免将测试点与两个侧面进行比较(其他答案中没有一种方法具有更低的成本,有些方法使其更糟糕,如15次减法和6次乘法,有时是除法)。
更新:使用剪切变换更快
如上所述,您可以使用两个比较快速地定位到由三个顶点坐标限定的四个水平带中的一个内部点。
您可以选择执行一到两个额外的X测试,以检查是否在边界框(虚线)内。
然后考虑由
X' = X - m Y,Y '= Y给出的“剪切”变换,其中m是最高边缘的斜率DX / DY。这个变换将使三角形的这一侧垂直。由于您知道在中间水平线的哪一侧,所以只需要相对于三角形的单侧进行符号测试即可。假设您预先计算了斜率
m,以及剪切三角形顶点的X'和边的方程系数,如X = m Y + p,在最坏的情况下,您将需要
- 两个纵坐标比较进行垂直分类;
- 可选的一到两个横坐标比较用于边界框拒绝;
X' = X - m Y的计算;- 与剪切三角形的横坐标进行一到两个比较;
- 与剪切三角形相关侧面的符号测试
X >< m' Y + p'。
1
这是最简单的概念,用来确定一个点是否在三角形内部或在三角形的一条边上。
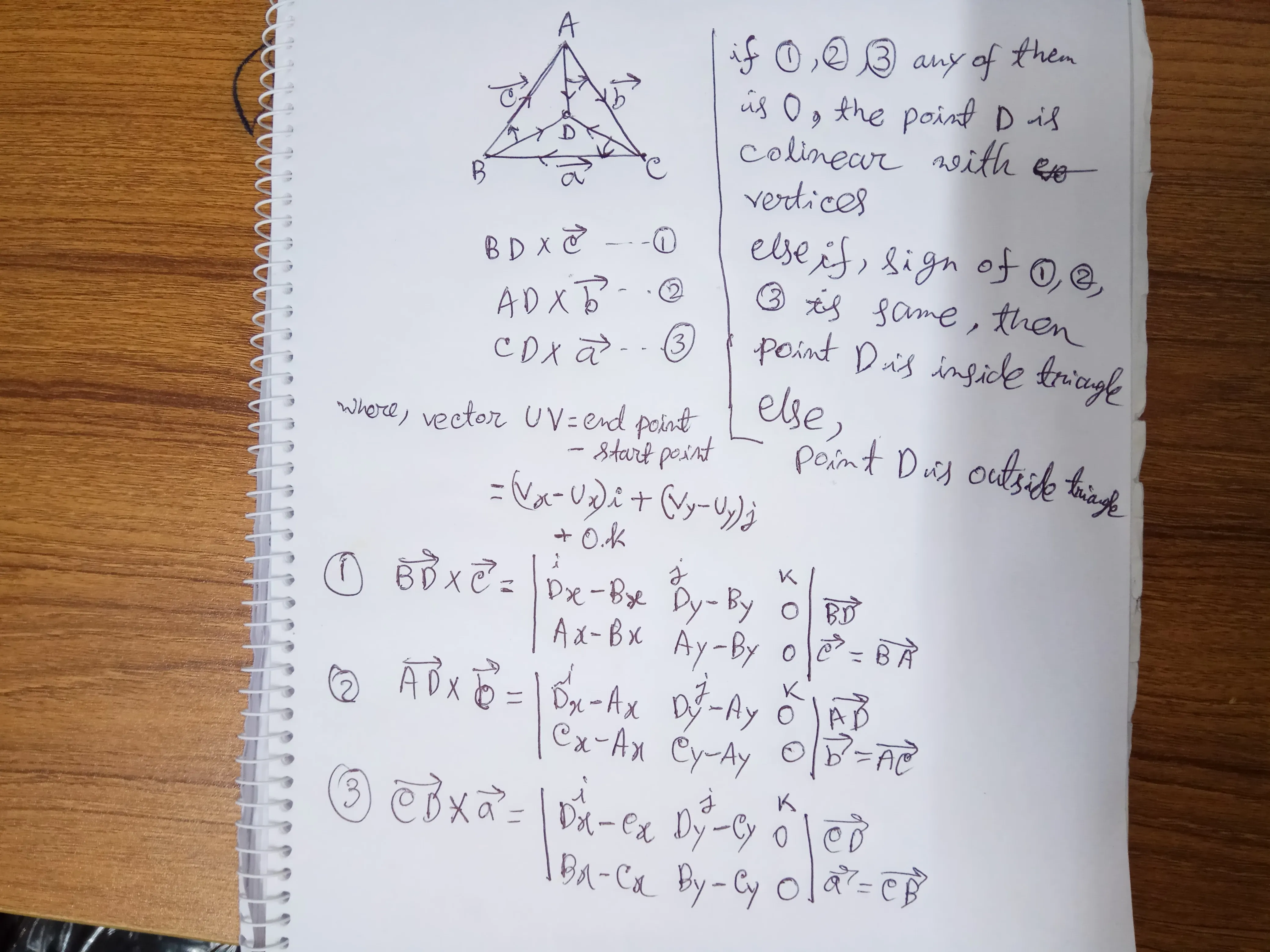
通过行列式确定一个点是否在三角形内部:
最简单的工作代码:
#-*- coding: utf-8 -*-
import numpy as np
tri_points = [(1,1),(2,3),(3,1)]
def pisinTri(point,tri_points):
Dx , Dy = point
A,B,C = tri_points
Ax, Ay = A
Bx, By = B
Cx, Cy = C
M1 = np.array([ [Dx - Bx, Dy - By, 0],
[Ax - Bx, Ay - By, 0],
[1 , 1 , 1]
])
M2 = np.array([ [Dx - Ax, Dy - Ay, 0],
[Cx - Ax, Cy - Ay, 0],
[1 , 1 , 1]
])
M3 = np.array([ [Dx - Cx, Dy - Cy, 0],
[Bx - Cx, By - Cy, 0],
[1 , 1 , 1]
])
M1 = np.linalg.det(M1)
M2 = np.linalg.det(M2)
M3 = np.linalg.det(M3)
print(M1,M2,M3)
if(M1 == 0 or M2 == 0 or M3 ==0):
print("Point: ",point," lies on the arms of Triangle")
elif((M1 > 0 and M2 > 0 and M3 > 0)or(M1 < 0 and M2 < 0 and M3 < 0)):
#if products is non 0 check if all of their sign is same
print("Point: ",point," lies inside the Triangle")
else:
print("Point: ",point," lies outside the Triangle")
print("Vertices of Triangle: ",tri_points)
points = [(0,0),(1,1),(2,3),(3,1),(2,2),(4,4),(1,0),(0,4)]
for c in points:
pisinTri(c,tri_points)
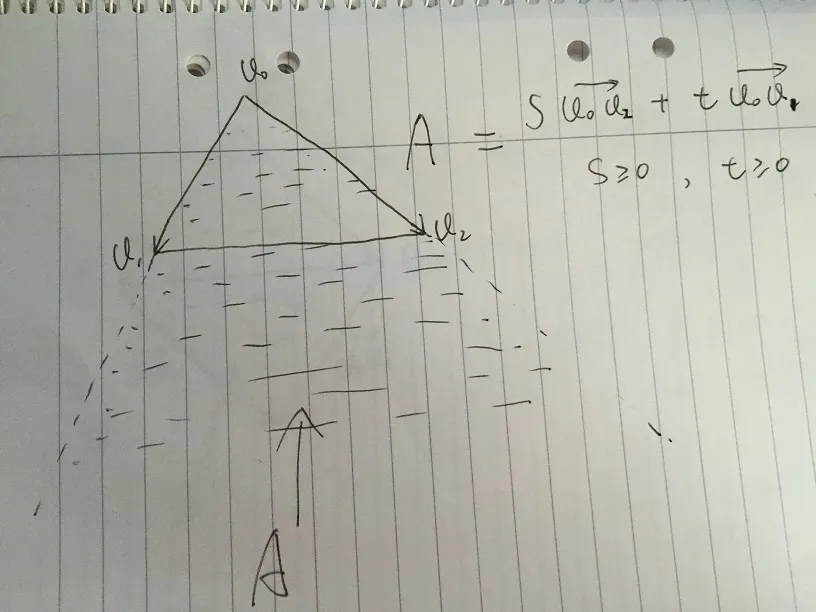
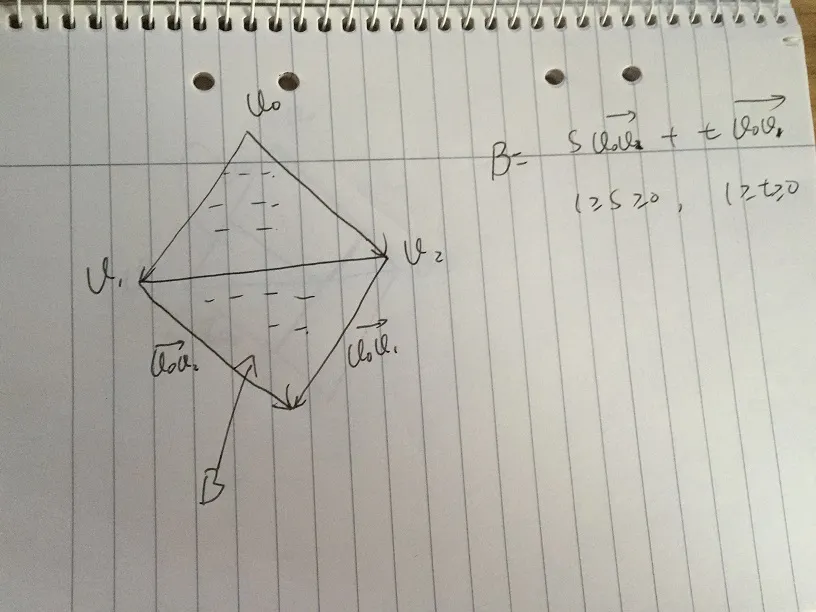
- 面积A被定义为任何向量,由s * v02 + t * v01给出,并满足条件s ≥ 0和t ≥ 0。如果有任何一个点在三角形v0、v1、v2内部,它必须在区域A内部。
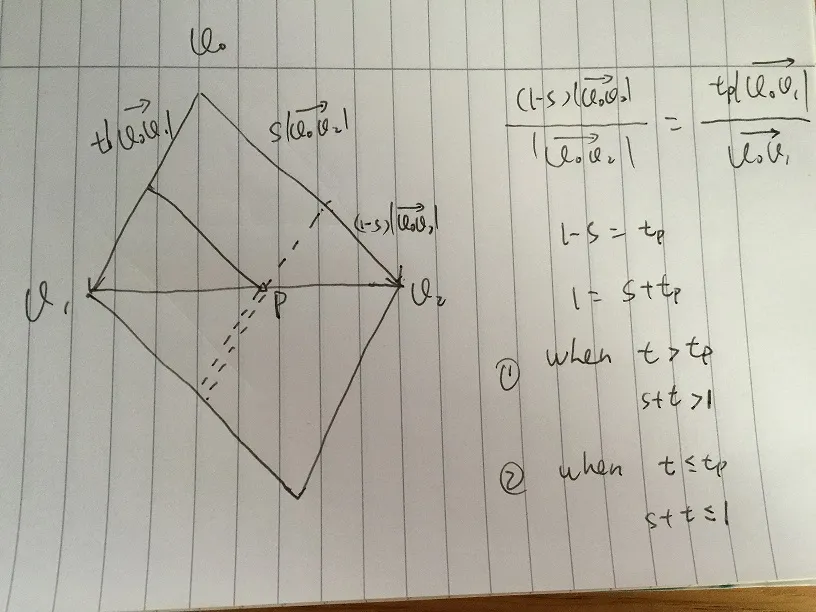
(1-s)|v0v2| / |v0v2| = tp|v0v1| / |v0v1|
我们得到1 - s = tp,然后1 = s + tp。如果任何t > tp,在双虚线上的1 < s + t的位置,向量在三角形外部;任何t <= tp,在单虚线上的1 >= s + t的位置,向量在三角形内部。
因此,如果我们给定任何s在[0,1]范围内,相应的t必须满足1 >= s + t,以使向量在三角形内部。 最终我们得到 v = s * v02 + t * v01,其中 v 在三角形内且满足条件 s、t、s+t 属于 [0, 1]。然后将其转化为点的形式,我们有: p - p0 = s * (p1 - p0) + t * (p2 - p0),其中 s、t、s+t 均属于 [0, 1]。
这与 Andreas 的解决方案相同,可以通过求解方程组 p = p0 + s * (p1 - p0) + t * (p2 - p0),其中 s、t、s+t 均属于 [0, 1] 来实现。
1
Python中的另一个函数,比开发者自己编写的方法更快(至少对我来说是这样),并且受到Cédric Dufour解决方案的启发:
def ptInTriang(p_test, p0, p1, p2):
dX = p_test[0] - p0[0]
dY = p_test[1] - p0[1]
dX20 = p2[0] - p0[0]
dY20 = p2[1] - p0[1]
dX10 = p1[0] - p0[0]
dY10 = p1[1] - p0[1]
s_p = (dY20*dX) - (dX20*dY)
t_p = (dX10*dY) - (dY10*dX)
D = (dX10*dY20) - (dY10*dX20)
if D > 0:
return ( (s_p >= 0) and (t_p >= 0) and (s_p + t_p) <= D )
else:
return ( (s_p <= 0) and (t_p <= 0) and (s_p + t_p) >= D )
你可以使用以下方法进行测试:
X_size = 64
Y_size = 64
ax_x = np.arange(X_size).astype(np.float32)
ax_y = np.arange(Y_size).astype(np.float32)
coords=np.meshgrid(ax_x,ax_y)
points_unif = (coords[0].reshape(X_size*Y_size,),coords[1].reshape(X_size*Y_size,))
p_test = np.array([0 , 0])
p0 = np.array([22 , 8])
p1 = np.array([12 , 55])
p2 = np.array([7 , 19])
fig = plt.figure(dpi=300)
for i in range(0,X_size*Y_size):
p_test[0] = points_unif[0][i]
p_test[1] = points_unif[1][i]
if ptInTriang(p_test, p0, p1, p2):
plt.plot(p_test[0], p_test[1], '.g')
else:
plt.plot(p_test[0], p_test[1], '.r')
绘制这个图表需要很多步骤,但是该网格与开发者代码相比,在0.0195319652557秒内进行了测试,而开发者代码则需要0.0844349861145秒。
最后,这段代码的注释:
# Using barycentric coordintes, any point inside can be described as:
# X = p0.x * r + p1.x * s + p2.x * t
# Y = p0.y * r + p1.y * s + p2.y * t
# with:
# r + s + t = 1 and 0 < r,s,t < 1
# then: r = 1 - s - t
# and then:
# X = p0.x * (1 - s - t) + p1.x * s + p2.x * t
# Y = p0.y * (1 - s - t) + p1.y * s + p2.y * t
#
# X = p0.x + (p1.x-p0.x) * s + (p2.x-p0.x) * t
# Y = p0.y + (p1.y-p0.y) * s + (p2.y-p0.y) * t
#
# X - p0.x = (p1.x-p0.x) * s + (p2.x-p0.x) * t
# Y - p0.y = (p1.y-p0.y) * s + (p2.y-p0.y) * t
#
# we have to solve:
#
# [ X - p0.x ] = [(p1.x-p0.x) (p2.x-p0.x)] * [ s ]
# [ Y - p0.Y ] [(p1.y-p0.y) (p2.y-p0.y)] [ t ]
#
# ---> b = A*x ; ---> x = A^-1 * b
#
# [ s ] = A^-1 * [ X - p0.x ]
# [ t ] [ Y - p0.Y ]
#
# A^-1 = 1/D * adj(A)
#
# The adjugate of A:
#
# adj(A) = [(p2.y-p0.y) -(p2.x-p0.x)]
# [-(p1.y-p0.y) (p1.x-p0.x)]
#
# The determinant of A:
#
# D = (p1.x-p0.x)*(p2.y-p0.y) - (p1.y-p0.y)*(p2.x-p0.x)
#
# Then:
#
# s_p = { (p2.y-p0.y)*(X - p0.x) - (p2.x-p0.x)*(Y - p0.Y) }
# t_p = { (p1.x-p0.x)*(Y - p0.Y) - (p1.y-p0.y)*(X - p0.x) }
#
# s = s_p / D
# t = t_p / D
#
# Recovering r:
#
# r = 1 - (s_p + t_p)/D
#
# Since we only want to know if it is insidem not the barycentric coordinate:
#
# 0 < 1 - (s_p + t_p)/D < 1
# 0 < (s_p + t_p)/D < 1
# 0 < (s_p + t_p) < D
#
# The condition is:
# if D > 0:
# s_p > 0 and t_p > 0 and (s_p + t_p) < D
# else:
# s_p < 0 and t_p < 0 and (s_p + t_p) > D
#
# s_p = { dY20*dX - dX20*dY }
# t_p = { dX10*dY - dY10*dX }
# D = dX10*dY20 - dY10*dX20
1
ptInTriang([11,45],[45, 45],[45, 45] ,[44, 45])会返回true,尽管它实际上是错误的。 - Code Pope如果点所在的线是水平的,请使用上方/下方。
如果该点位于多个三角形的公共顶点上,请使用以该点为中心形成最小角度的三角形。
更有趣的是:三个点可以在一条直线上(零度),例如(0,0)-(0,10)-(0,5)。在三角剖分算法中,“耳朵”(0,10)必须被去掉,生成的“三角形”是一条直线的退化情况。
bool isInside( float x, float y, float x1, float y1, float x2, float y2, float x3, float y3 ) {
float l1 = (x-x1)*(y3-y1) - (x3-x1)*(y-y1),
l2 = (x-x2)*(y1-y2) - (x1-x2)*(y-y2),
l3 = (x-x3)*(y2-y3) - (x2-x3)*(y-y3);
return (l1>0 && l2>0 && l3>0) || (l1<0 && l2<0 && l3<0);
}
没有比这更高效的了!三角形的每一边都可以拥有独立的位置和方向,因此需要三个计算:l1、l2和l3,每个计算涉及2次乘法。一旦知道了l1、l2和l3,结果只需要进行几个基本的比较和布尔运算即可。
我需要在“可控环境”中进行三角形点检查,当你绝对确定三角形是顺时针的时候。因此,我采用了Perro Azul的jsfiddle,并按照coproc的建议对其进行了修改,以适应这种情况;同时删除了多余的0.5和2乘法,因为它们只会相互抵消。
http://jsfiddle.net/dog_funtom/H7D7g/
var ctx = $("canvas")[0].getContext("2d");
var W = 500;
var H = 500;
var point = {
x: W / 2,
y: H / 2
};
var triangle = randomTriangle();
$("canvas").click(function (evt) {
point.x = evt.pageX - $(this).offset().left;
point.y = evt.pageY - $(this).offset().top;
test();
});
$("canvas").dblclick(function (evt) {
triangle = randomTriangle();
test();
});
test();
function test() {
var result = ptInTriangle(point, triangle.a, triangle.b, triangle.c);
var info = "point = (" + point.x + "," + point.y + ")\n";
info += "triangle.a = (" + triangle.a.x + "," + triangle.a.y + ")\n";
info += "triangle.b = (" + triangle.b.x + "," + triangle.b.y + ")\n";
info += "triangle.c = (" + triangle.c.x + "," + triangle.c.y + ")\n";
info += "result = " + (result ? "true" : "false");
$("#result").text(info);
render();
}
function ptInTriangle(p, p0, p1, p2) {
var s = (p0.y * p2.x - p0.x * p2.y + (p2.y - p0.y) * p.x + (p0.x - p2.x) * p.y);
var t = (p0.x * p1.y - p0.y * p1.x + (p0.y - p1.y) * p.x + (p1.x - p0.x) * p.y);
if (s <= 0 || t <= 0) return false;
var A = (-p1.y * p2.x + p0.y * (-p1.x + p2.x) + p0.x * (p1.y - p2.y) + p1.x * p2.y);
return (s + t) < A;
}
function checkClockwise(p0, p1, p2) {
var A = (-p1.y * p2.x + p0.y * (-p1.x + p2.x) + p0.x * (p1.y - p2.y) + p1.x * p2.y);
return A > 0;
}
function render() {
ctx.fillStyle = "#CCC";
ctx.fillRect(0, 0, 500, 500);
drawTriangle(triangle.a, triangle.b, triangle.c);
drawPoint(point);
}
function drawTriangle(p0, p1, p2) {
ctx.fillStyle = "#999";
ctx.beginPath();
ctx.moveTo(p0.x, p0.y);
ctx.lineTo(p1.x, p1.y);
ctx.lineTo(p2.x, p2.y);
ctx.closePath();
ctx.fill();
ctx.fillStyle = "#000";
ctx.font = "12px monospace";
ctx.fillText("1", p0.x, p0.y);
ctx.fillText("2", p1.x, p1.y);
ctx.fillText("3", p2.x, p2.y);
}
function drawPoint(p) {
ctx.fillStyle = "#F00";
ctx.beginPath();
ctx.arc(p.x, p.y, 5, 0, 2 * Math.PI);
ctx.fill();
}
function rand(min, max) {
return Math.floor(Math.random() * (max - min + 1)) + min;
}
function randomTriangle() {
while (true) {
var result = {
a: {
x: rand(0, W),
y: rand(0, H)
},
b: {
x: rand(0, W),
y: rand(0, H)
},
c: {
x: rand(0, W),
y: rand(0, H)
}
};
if (checkClockwise(result.a, result.b, result.c)) return result;
}
}<script src="https://cdnjs.cloudflare.com/ajax/libs/jquery/1.9.1/jquery.min.js"></script>
<pre>Click: place the point.
Double click: random triangle.</pre>
<pre id="result"></pre>
<canvas width="500" height="500"></canvas>public static bool IsPointInClockwiseTriangle(Vector2 p, Vector2 p0, Vector2 p1, Vector2 p2)
{
var s = (p0.y * p2.x - p0.x * p2.y + (p2.y - p0.y) * p.x + (p0.x - p2.x) * p.y);
var t = (p0.x * p1.y - p0.y * p1.x + (p0.y - p1.y) * p.x + (p1.x - p0.x) * p.y);
if (s <= 0 || t <= 0)
return false;
var A = (-p1.y * p2.x + p0.y * (-p1.x + p2.x) + p0.x * (p1.y - p2.y) + p1.x * p2.y);
return (s + t) < A;
}
原文链接