假设您有一个浮点数列表，这些数大致上是某个公共量的倍数，例如：
2.468、3.700、6.1699
它们大致上都是1.234的倍数。如何描述这个"近似最大公约数"，并如何继续计算或估计它？
这与我在此问题的回答密切相关。
2.468、3.700、6.1699
它们大致上都是1.234的倍数。如何描述这个"近似最大公约数"，并如何继续计算或估计它？
这与我在此问题的回答密切相关。
"近似"最大公约数
47
- Federico Ramponi
1
2从你之前的问题中可以看出，你正在检测钢琴音调的频率。请注意，钢琴并不是谐波的。高频率从一开始就不是基频的整数倍：它们略微偏高，因为弦在高频率下的行为就像它的长度更短一样。因此，钢琴调音师会略微拉伸音阶，以最小化部分间的拍动，并最大化和声：https://en.wikipedia.org/wiki/Inharmonicity#Pianos - endolith
8个回答
25
你可以使用欧几里得的gcd算法，将任何小于0.01（或您选择的一个小数）的数视为伪0。对于你的数字：
3.700 = 1 * 2.468 + 1.232,
2.468 = 2 * 1.232 + 0.004.
因此，前两个数字的伪gcd为1.232。现在你需要用它和最后一个数求gcd：
6.1699 = 5 * 1.232 + 0.0099.
因此1.232是伪gcd，它的倍数是2、3、5。为了改善这个结果，可以对数据点进行线性回归：
(2,2.468), (3,3.7), (5,6.1699).
斜率是改进后的伪gcd。
注意：该算法的第一部分在数值上不稳定 - 如果你从非常脏的数据开始，那么可能会出问题。
- David Lehavi
14
将测量值表示为最低值的倍数。因此，您的列表变为1.00000、1.49919、2.49996。这些值的小数部分将非常接近于1/Nths，其中N的值由最低值与基频之间的接近程度决定。建议您循环增加N，直到找到足够精细的匹配为止。在此情况下，对于N=1（即假设X=2.468是您的基频）, 您会发现标准偏差为0.3333（三个值中有两个与X* 1相差0.5），这是不可接受的。对于N=2（即假设2.468/2是您的基频），您会发现标准偏差几乎为零（所有三个值都与X/2的倍数相差不到0.001），因此2.468/2是您的近似GCD。
我的计划的主要缺陷在于它在最低测量值最准确时效果最好，但这可能不是情况。这可以通过多次执行整个操作并每次丢弃测量值列表中的最低值来减轻，然后使用每次操作的结果列表来确定更精确的结果。另一种改进结果的方法是调整GCD以最小化GCD的整数倍与测量值之间的标准偏差。
我的计划的主要缺陷在于它在最低测量值最准确时效果最好，但这可能不是情况。这可以通过多次执行整个操作并每次丢弃测量值列表中的最低值来减轻，然后使用每次操作的结果列表来确定更精确的结果。另一种改进结果的方法是调整GCD以最小化GCD的整数倍与测量值之间的标准偏差。
- Sparr
14
这让我想起了寻找实数的良好有理数逼近问题。标准技术是使用连分数展开：
def rationalizations(x):
assert 0 <= x
ix = int(x)
yield ix, 1
if x == ix: return
for numer, denom in rationalizations(1.0/(x-ix)):
yield denom + ix * numer, numer
>>> a, b, c = 2.468, 3.700, 6.1699
>>> b/a, c/a
(1.4991896272285252, 2.4999594813614263)
>>> list(itertools.islice(rationalizations(b/a), 3))
[(1, 1), (3, 2), (925, 617)]
>>> list(itertools.islice(rationalizations(c/a), 3))
[(2, 1), (5, 2), (30847, 12339)]
д»ҺжҜҸдёӘеәҸеҲ—дёӯеҸ–еҮә第дёҖдёӘи¶іеӨҹеҘҪзҡ„иҝ‘дјјеҖјгҖӮпјҲиҝҷйҮҢжҳҜ3/2е’Ң5/2гҖӮпјүжҲ–иҖ…пјҢдҪ еҸҜд»ҘжіЁж„ҸеҲ°925/617дҪҝз”ЁжҜ”3/2жӣҙеӨ§зҡ„ж•ҙж•°пјҢдҪҝеҫ—3/2жҲҗдёәдёҖдёӘеҫҲеҘҪзҡ„еҒңжӯўзӮ№пјҢиҖҢдёҚжҳҜзӣҙжҺҘе°Ҷ3.0/2.0дёҺ1.499189...иҝӣиЎҢжҜ”иҫғгҖӮ
дҪ йҖүжӢ©з”Ёе“ӘдёӘж•°еӯ—йҷӨд»ҘеҸҰдёҖдёӘ并дёҚеӨӘйҮҚиҰҒгҖӮпјҲдҫӢеҰӮпјҢдҪҝз”Ёa/bе’Ңc/bдҪ дјҡеҫ—еҲ°2/3е’Ң5/3гҖӮпјүдёҖж—ҰдҪ жңүдәҶж•ҙж•°жҜ”зҺҮпјҢдҪ еҸҜд»ҘйҖҡиҝҮshsmurfyзҡ„зәҝжҖ§еӣһеҪ’жқҘж”№иҝӣеҜ№еҹәжң¬йў‘зҺҮзҡ„дј°и®ЎгҖӮжҜҸдёӘдәәйғҪиҺ·иғңпјҒ
- Darius Bacon
5
我假设你的所有数字都是整数的倍数。在我的解释中，A代表你要找到的“根”频率，B是你需要开始处理的数字数组。
你要做的事情表面上与线性回归相似。你正在尝试找到一个线性模型y=mx+b，该模型最小化线性模型和一组数据之间的平均距离。在你的情况下，b=0，m是根频率，y表示给定的值。最大的问题是独立变量X没有明确给出。我们唯一知道的关于X的事情是它的所有成员都必须是整数。
你的第一个任务是确定这些独立变量。我目前能想到的最好方法是假设给定的频率具有接近连续的索引（
如果你想更好地近似根频率A，现在你已经有了相应的依赖变量，你可以使用线性回归最小化线性模型的误差。最简单的方法是使用最小二乘拟合。 Wolfram's Mathworld对这个问题进行了深入的数学处理，但是通过一些谷歌搜索，可以找到相当简单的解释。
你要做的事情表面上与线性回归相似。你正在尝试找到一个线性模型y=mx+b，该模型最小化线性模型和一组数据之间的平均距离。在你的情况下，b=0，m是根频率，y表示给定的值。最大的问题是独立变量X没有明确给出。我们唯一知道的关于X的事情是它的所有成员都必须是整数。
你的第一个任务是确定这些独立变量。我目前能想到的最好方法是假设给定的频率具有接近连续的索引（
x_1=x_0+n）。因此，B_0/B_1=(x_0)/(x_0+n)给定一个（希望）较小的整数n。然后，你可以利用这样一个事实：x_0 = n/(B_1-B_0)，从n=1开始，并不断地提高它，直到k-rnd(k)在某个阈值内。当你有了x_0（初始索引）之后，你可以近似计算根频率（A = B_0/x_0）。然后，你可以通过找到x_n = rnd(B_n/A)来近似计算其他索引。这种方法不太健壮，如果数据误差很大，可能会失败。如果你想更好地近似根频率A，现在你已经有了相应的依赖变量，你可以使用线性回归最小化线性模型的误差。最简单的方法是使用最小二乘拟合。 Wolfram's Mathworld对这个问题进行了深入的数学处理，但是通过一些谷歌搜索，可以找到相当简单的解释。
- shsmurfy
4
有趣的问题...不太容易。
我想我会看样本值的比率：
3.700 / 2.468 = 1.499...
6.1699 / 2.468 = 2.4999...
6.1699 / 3.700 = 1.6675...
然后我会寻找这些结果中的简单整数比率。
1.499≈3/2
2.4999≈5/2
1.6675≈5/3
我没有追踪它，但在某个地方，你决定1：1000左右的误差就够了，然后通过回溯找到基本近似GCD。
我想我会看样本值的比率：
3.700 / 2.468 = 1.499...
6.1699 / 2.468 = 2.4999...
6.1699 / 3.700 = 1.6675...
然后我会寻找这些结果中的简单整数比率。
1.499≈3/2
2.4999≈5/2
1.6675≈5/3
我没有追踪它，但在某个地方，你决定1：1000左右的误差就够了，然后通过回溯找到基本近似GCD。
- Jonathan Leffler
3
我见过并且自己也使用过的解决方案是选择一个常数，比如1000，将所有数字乘以这个常数，四舍五入为整数，使用标准算法找到这些整数的最大公约数，然后将结果除以该常数（1000）。常数越大，精度越高。
- quant_dev
1
如果其中一个数字有非常微小的错误，例如
1.234,2.468 可以得到 1.234，但是 1.234,2.467 却只能得到 0.001，这种方法就行不通了。 - user2027291
这是对shsmurfy解决方案的改写，当你预先选择3个正公差（e1、e2、e3）时。
问题是要寻找最小的正整数（n1、n2、n3），从而确定最大的根频率f，使得：
f1 = n1*f +/- e1
f2 = n2*f +/- e2
f3 = n3*f +/- e3
我们假设 0 <= f1 <= f2 <= f3
如果我们固定 n1，那么我们得到以下关系：
f is in interval I1=[(f1-e1)/n1 , (f1+e1)/n1]
n2 is in interval I2=[n1*(f2-e2)/(f1+e1) , n1*(f2+e2)/(f1-e1)]
n3 is in interval I3=[n1*(f3-e3)/(f1+e1) , n1*(f3+e3)/(f1-e1)]
我们从n1 = 1开始，然后递增n1直到区间I2和I3包含一个整数 - 即
floor(I2min)不等于floor(I2max)，I3同理。然后我们选择区间I2中最小的整数n2和区间I3中最小的整数n3。
假设浮点误差服从正态分布，则根频率f的最可能估计是最小化的。
J = (f1/n1 - f)^2 + (f2/n2 - f)^2 + (f3/n3 - f)^2
那就是
f = (f1/n1 + f2/n2 + f3/n3)/3
如果在区间I2，I3中有多个整数n2，n3，我们也可以选择使余数最小的一对。
min(J)*3/2=(f1/n1)^2+(f2/n2)^2+(f3/n3)^2-(f1/n1)*(f2/n2)-(f1/n1)*(f3/n3)-(f2/n2)*(f3/n3)
另一种变体可能是继续迭代并尝试最小化另一个标准，例如min(J(n1))*n1，直到f降至某个频率（n1达到上限）...
- aka.nice
1
我在MathStackExchange上找到了这个问题，寻找答案以解决自己的问题 (这里 和 这里)。
目前我只能测量基频的吸引力，给定一组谐波频率(遵循声音/音乐术语)，如果您的选择有限且计算每个选项的吸引力然后选择最佳匹配是可行的，则此方法可能会有用。
以下是我在MSE中的问题(C&P)(在那里格式更漂亮):
目前我只能测量基频的吸引力，给定一组谐波频率(遵循声音/音乐术语)，如果您的选择有限且计算每个选项的吸引力然后选择最佳匹配是可行的，则此方法可能会有用。
以下是我在MSE中的问题(C&P)(在那里格式更漂亮):
- 将列表{v_1, v_2, ..., v_n}从小到大排序，得到有序列表being v
- mean_sin(v, x) = 对于i∈{1, ...,n}，求和sin(2*pi*v_i/x)，再除以n
- mean_cos(v, x) = 对于i∈{1, ...,n}，求和cos(2*pi*v_i/x)，再除以n
- gcd_appeal(v, x) = 1 - sqrt(mean_sin(v, x)^2 + (mean_cos(v, x) - 1)^2)/2，它会返回区间[0,1]中的一个数。
目标是找到最大吸引力的x值。下方是你的例子[2.468, 3.700, 6.1699]的(gcd_appeal)图像。我们可以发现，最优GCD出现在x = 1.2337899957639993处。
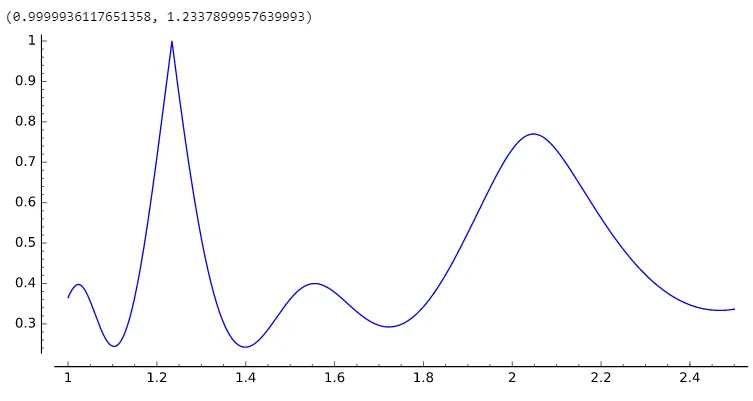
编辑： 你可能会发现这段JAVA代码很有用，它可以计算除数相对于一组被除数的（模糊）可除性（也称为gcd_appeal）；你可以使用它来测试哪个候选者是最好的除数。 代码看起来很丑，因为我试图优化它的性能。
//returns the mean divisibility of dividend/divisor as a value in the range [0 and 1]
// 0 means no divisibility at all
// 1 means full divisibility
public double divisibility(double divisor, double... dividends) {
double n = dividends.length;
double factor = 2.0 / divisor;
double sum_x = -n;
double sum_y = 0.0;
double[] coord = new double[2];
for (double v : dividends) {
coordinates(v * factor, coord);
sum_x += coord[0];
sum_y += coord[1];
}
double err = 1.0 - Math.sqrt(sum_x * sum_x + sum_y * sum_y) / (2.0 * n);
//Might happen due to approximation error
return err >= 0.0 ? err : 0.0;
}
private void coordinates(double x, double[] out) {
//Bhaskara performant approximation to
//out[0] = Math.cos(Math.PI*x);
//out[1] = Math.sin(Math.PI*x);
long cos_int_part = (long) (x + 0.5);
long sin_int_part = (long) x;
double rem = x - cos_int_part;
if (cos_int_part != sin_int_part) {
double common_s = 4.0 * rem;
double cos_rem_s = common_s * rem - 1.0;
double sin_rem_s = cos_rem_s + common_s + 1.0;
out[0] = (((cos_int_part & 1L) * 8L - 4L) * cos_rem_s) / (cos_rem_s + 5.0);
out[1] = (((sin_int_part & 1L) * 8L - 4L) * sin_rem_s) / (sin_rem_s + 5.0);
} else {
double common_s = 4.0 * rem - 4.0;
double sin_rem_s = common_s * rem;
double cos_rem_s = sin_rem_s + common_s + 3.0;
double common_2 = ((cos_int_part & 1L) * 8L - 4L);
out[0] = (common_2 * cos_rem_s) / (cos_rem_s + 5.0);
out[1] = (common_2 * sin_rem_s) / (sin_rem_s + 5.0);
}
}
- jmmurillo
网页内容由stack overflow 提供, 点击上面的可以查看英文原文，
原文链接
原文链接