由于顶点的最大长度可以为sqrt(2),我们可以假设我们的图需要存在于网格世界中,其中节点具有正整数x和y坐标,并且顶点只能连接附近的节点,受长度限制。
解决方案是逐个扩展组件,使用带来组件更接近的节点和顶点。该问题的连通图将添加节点9和10以及连接的顶点。请参见下面的第一张图片。
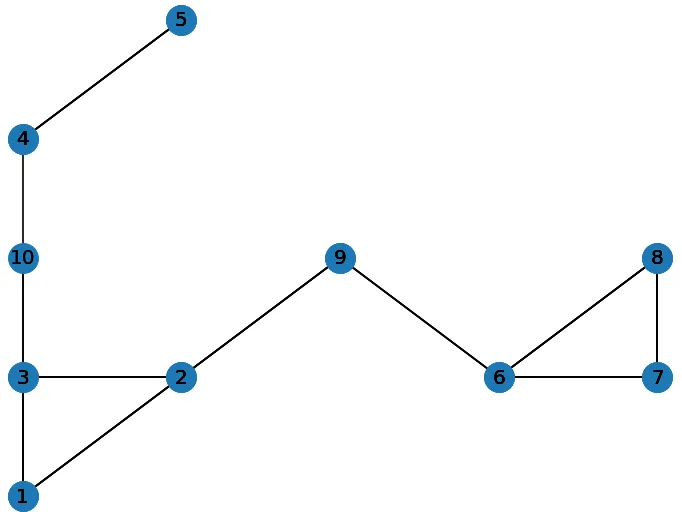
除了OP问题中提到的测试之外,似乎更有趣的测试是将节点4放置在位置(3,4)。在这种情况下,最优解是一个斯坦纳点(参见
enter link description here)。
为了构建这样的小图解决方案,我们可以使用一种算法,添加一个节点和一条连接最近的一对节点之一的边缘。为了适应构建斯坦纳树,我们允许在对角线位置选择点的位置。也就是说,节点2和6具有相同的y坐标,但我们将对角线地创建节点9,以便我们可以建立到下一个最近邻居的桥梁。请参见下面的图片。
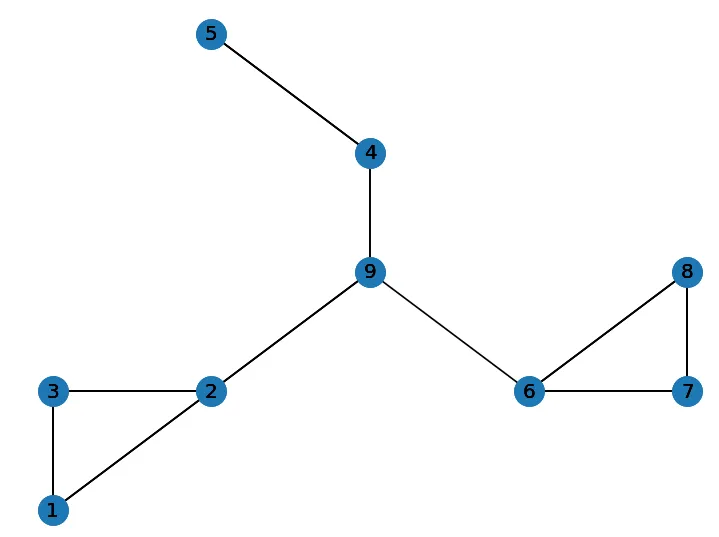
为了避免建立额外的节点,应该逐步添加节点。由于我们已经给节点编号,因此可以通过选择最小的节点编号来进行操作。这会导致在需要跨越更多空间时生长更大的斯坦纳树。请参见下图,在原始图中添加节点9到12。
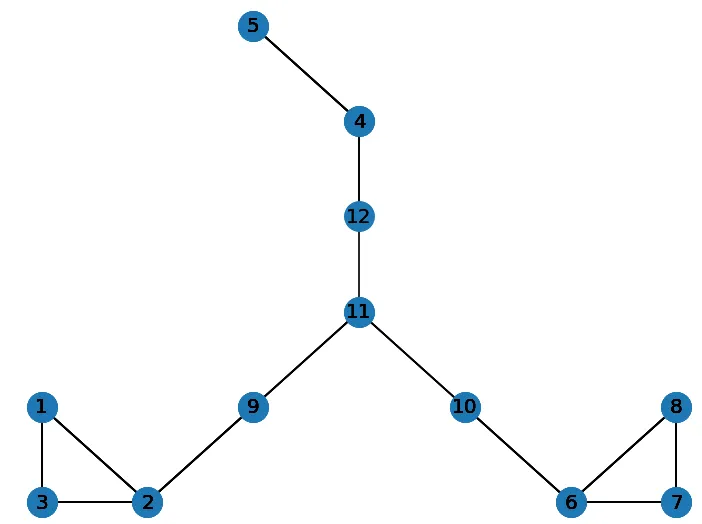
这个(且非常低效的)粗略算法如下所示。欧几里得距离函数是从Russell&Norvig(Stuart Russell和Peter Norvig的“人工智能现代方法”Github库)修改而来的。
import itertools
import networkx as nx
import numpy as np
def closest_nodes(c1, c2, components):
nodes_c1 = [(n, G.nodes[n]['pos']) for n in components[c1]]
nodes_c2 = [(n,G.nodes[n]['pos']) for n in components[c2]]
xnodes = itertools.product(nodes_c1, nodes_c2)
closest = min(xnodes, key=lambda x: euclidean_distance(x[0], x[1]))
return euclidean_distance(closest[0], closest[1]), closest
def next_closest_node(n1, c1, c2, components):
other_nodes = []
for i,v in enumerate(components):
if i == c1 or i == c2:
continue
other_nodes.extend((n, G.nodes[n]['pos']) for n in v)
if len(other_nodes) == 0:
return None
closest = min(other_nodes, key=lambda x: euclidean_distance(x, n1))
return closest
def closest_comps(components):
xcomps = itertools.combinations(range(len(components)), 2)
closest = min(xcomps,
key=lambda x: closest_nodes(x[0], x[1], components)[0])
return closest
def euclidean_distance(x, y):
xc = x[1]
yc = y[1]
return np.sqrt(sum((_x - _y) ** 2 for _x, _y in zip(xc, yc)))
def determine_pos(sel_comps, sel_nodes, components):
next_closest = next_closest_node(sel_nodes[1][0], *sel_comps, components)
if sel_nodes[1][0][0] < sel_nodes[1][1][0]:
from_node = sel_nodes[1][0][0]
start_pos = sel_nodes[1][0][1]
target_pos = sel_nodes[1][1][1]
else:
from_node = sel_nodes[1][1][0]
start_pos = sel_nodes[1][1][1]
target_pos = sel_nodes[1][0][1]
diff_x = target_pos[0]-start_pos[0]
diff_y = target_pos[1]-start_pos[1]
new_x, new_y = start_pos[0], start_pos[1]
if diff_x != 0:
new_x += diff_x//abs(diff_x)
elif next_closest is not None:
diff_x = next_closest[1][0]-start_pos[0]
if diff_x != 0:
new_x += diff_x//abs(diff_x)
if diff_y != 0:
new_y += diff_y//abs(diff_y)
elif next_closest is not None:
diff_y = next_closest[1][1]-start_pos[1]
if diff_y != 0:
new_y += diff_y//abs(diff_y)
return from_node, (new_x, new_y)
while not nx.is_connected(G):
components = [c for c in
sorted(nx.connected_components(G), key=len, reverse=True)]
sel_comps = closest_comps(components)
sel_nodes = closest_nodes(*sel_comps, components)
sel_dist = euclidean_distance(sel_nodes[1][0], sel_nodes[1][1])
edge_needed = sel_dist <= np.sqrt(2)
if edge_needed:
G.add_edge(sel_nodes[1][0][0], sel_nodes[1][1][0])
else:
new_pos = determine_pos(sel_comps, sel_nodes, components)
new_node = G.number_of_nodes() + 1
G.add_node(new_node, pos=new_pos[1])
G.add_edge(new_pos[0], new_node)
pos = nx.get_node_attributes(G, 'pos')
nx.draw(G, pos, with_labels=True)
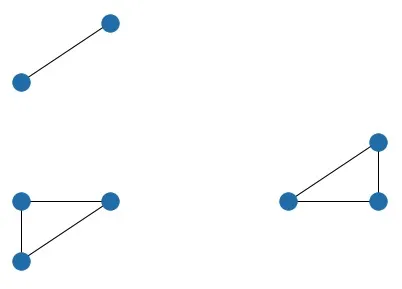



sqrt(2)。在最坏的情况下,您将不得不在整个周长上创建节点,直到所有节点都连接起来。 - jylls