在这种情况下，动态规划和记忆化的复杂度有何不同？

Question

在这种情况下，动态规划和记忆化的复杂度有何不同？

javaalgorithmbig-otime-complexitydynamic-programming

3

我正在进行一项关于动态规划的小练习。我有以下函数：

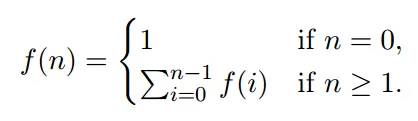
enter image description here

我需要使用两种方法（带备忘录的自顶向下和自底向上）来编写此函数。

这是我目前为自底向上所做的：

    public static int functionBottomUp (int n){
            int [] array = new int[n+1];
            array[0] = 1;
            for(int i = 1; i < array.length; i++){
                if(i == 1)
                    array[i] = array[i - 1];
                else {
                    for(int p = 0; p < i; p ++)
                        array[i] += array[p];
                }
            }
            return array[n];
   }

对于记忆化：

public static int functionMemoization(int n){
        int[] array = new int[n+1];     
        for(int i = 0; i < n; i++)
            array[i] = 0;
        return compute(array, n);
    }

    private static int compute(int[] array, int n){
        int ans = 0;
        if(array[n] > 0)
            return array[n];
        if(n == 0 || n == 1)
            ans = 1;
        else 
            for(int i = 0; i < n; i++)
                ans += compute(array, i);
        array[n] = ans;
        return array[n];
    }

我正确地得到了两个函数的输出，但现在我很困惑如何计算它们的复杂度。

首先，f(n) 的复杂度是 2^n，因为 f(3) 对 f(0) 调用 7 次，而 f(4) 对 f(0) 调用 15 次（我知道这不是一个正式的证明，但这只是给我一个概念）。

但现在我卡在了计算两个函数复杂度上。

自下而上：

我认为复杂度是 O(n)（因为有 for(int i = 1; i < array.length; i++)），但是有内部循环 for(int p = 0; p < i; p ++) 我不知道这是否会修改复杂度。

备忘录法：

显然，由于第一个循环初始化数组，这个复杂度至少是 O(n)。但是我不知道 compute 函数会如何修改这个复杂度。

能否有人为我解释一下？

- user2336315

1

你有没有考虑过这个事实，即 f(n) = 2^(n-1)，n>=1？ - sve

1个回答

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- templatetypedef · Accepted Answer

让我们来看看您的函数。这是自底向上的 DP 版本：

public static int functionBottomUp (int n){
        int [] array = new int[n+1];
        array[0] = 1;
        for(int i = 1; i < array.length; i++){
            if(i == 1)
                array[i] = array[i - 1];
            else {
                for(int p = 0; p < i; p ++)
                    array[i] += array[p];
            }
        }
        return array[n];
}

为了统计正在进行的工作量，我们可以看一下完成任意i循环迭代所需的工作量。注意，如果i=1，则完成的工作量为O(1)。否则，循环运行时间将由此部分占用：

for(int p = 0; p < i; p ++)
    array[i] += array[p];

这个循环的时间复杂度与i成正比。这意味着循环迭代i需要（或多或少）i个单位的工作量。因此，总工作量约为:

1 + 2 + 3 + ... + n = Θ(n²)

因此，这里的运行时间是Θ(n²), 而不是你在问题中猜测的O(n)。

现在，让我们看一下自顶向下的版本:

public static int functionMemoization(int n){
    int[] array = new int[n+1];     
    for(int i = 0; i < n; i++)
        array[i] = 0;
    return compute(array, n);
}

private static int compute(int[] array, int n){
    int ans = 0;
    if(array[n] > 0)
        return array[n];
    if(n == 0 || n == 1)
        ans = 1;
    else 
        for(int i = 0; i < n; i++)
            ans += compute(array, i);
    array[n] = ans;
    return array[n];
}

您最初需要做Θ(n)的工作来清空数组，然后调用compute计算所有值。最终您将填充array中的所有值，并且每个数组元素只会填充一次，因此确定时间复杂度的一种方法是确定每个数组条目需要多少工作才能填充。在这种情况下，完成的工作由以下部分确定：

for(int i = 0; i < n; i++)
    ans += compute(array, i);

由于您正在记忆值，因此在确定对值n计算函数所需的工作量时，我们可以假装每个递归调用需要O(1)的时间；当我们跨所有n求和时，实际工作将被考虑在内。与之前一样，这里所做的工作与n成比例。因此，由于n范围从1到n，所做的工作大致为：

1 + 2 + 3 + ... + n = Θ(n²)

再次说明，这比您估计的O(n)更耗费工作量。

然而，有一种更快的方法来评估这个递归式。看一下f(n)的前几个值：

f(0) = 1 f(1) = 1 f(2) = 2 f(3) = 4 f(4) = 8 f(5) = 16 ... f(n) = 2^(n-1)

因此，我们得到：

f(0) = 1 如果n > 0，则f(n) = 2^(n-1)

因此，以下函数评估f时间：

int f(int n) {
    return n == 0? 1 : 1 << (n - 1);
}

假设您正在使用固定大小的整数（例如32位或64位整数），这需要时间O（1）。如果您正在使用任意精度的整数，则需要时间Θ（n），因为您不能在不写出Θ（n）位的情况下表示2 ^n-1，但是如果我们在此假设下运行，原始代码的运行时间也需要进行调整以考虑加法的成本。为简单起见，我将忽略它或将其留给读者练习。^_^希望这可以帮助您！