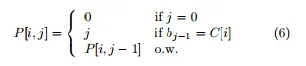我正试图实现《最长公共子序列问题的并行算法》，该算法在http://www.iaeng.org/publication/WCE2010/WCE2010_pp499-504.pdf中有详细描述。
但是我在第4页的第6个方程式中遇到了C变量的问题。
论文在第3页末尾提到C如下：
C是有限字母表，C[1:l]代表它。
我不确定这意味着什么，因为我猜如果它用于两个字符串ABCDEF和ABQXYEF，那么结果应该是ABCDEFQXY。但如果我的两个字符串是一个对象列表（例如，我的匹配测试为obj1.Name = obj2.Name），那么C会是什么？只是两个数组的联合吗？
C应该是一个数组，保存字符串的字母表，其中字母表大小（因此C的大小）为l。P[i,j]是什么，为什么需要它呢？答案是您不真正需要它，但这是一种优雅的优化。在第3页，在Theorem 1之前稍微说了一下：[...]当第k步时，j-k = 0或a(i) = b(j-k)。假设过程在第k步停止，k必须是使a(i) = b(j-k)或j-k = 0的最小数字。
式（3）中的递归关系等同于式（2），但根本区别在于式（2）会递归扩展，而对于式（3），只要您知道k，就不会有递归调用。换句话说，(3)不会递归地扩展的魔力是您以某种方式知道递归在(2)上将停止的位置，因此您立即查看该单元格，而不是以递归方式接近它。k的值呢？由于k是（2）达到基本情况的位置，因此可以看出k是您必须“回退”B的列数，直到您要么超出范围（即第一列填充为0的情况），要么在B中找到一个匹配A中字符的字符（这对应于（2）中的基本情况条件）。请记住，您将匹配字符a(i-1)，其中i是当前行。j之前的B中最后一个出现字符a(i-1)的位置。如果在j之前没有这样的字符出现在B中，则相当于在(2)中达到i = 0或j-1 = 0的情况；否则，就相当于在(2)中达到a(i) = b(j-1)的情况。P[i,j]的整个思想。 P 是一个表格，在左侧垂直地排列整个字母表；字符串B再次水平地放置在上方。该表格作为预处理步骤的一部分进行计算，它将精确地告诉您需要提前了解的内容：对于B中的每个位置j，它��对于C（字母表）中的每个字符C[i]，在j之前B中找到C[i]的最后位置是什么（请注意，索引i用于索引C，即字母表，而不是字符串A。也许作者应该使用另一个索引变量来避免混淆)。
因此，您可以将条目P[i,j]的语义视为以下行：“在位置j之前，我看到C[i]的B中的最后位置”。例如，如果您的字母表是sigma = {A, E, I, O, U}，并且B = "AOOIUEI"，那么P`如下：
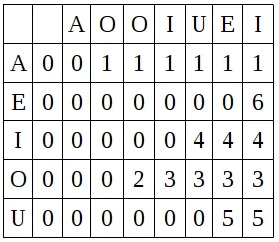
花些时间理解这张表。注意O的行。记住：该行列出了B中每个位置最后一个已知“O”的位置。仅当j = 3时，我们才会有一个不为零的值（它是2），因为这是在AOOIUEI中第一个O之后的位置。此条目表示，在j = 3之前，在B中看到O的最后位置是位置2（确实，B[2]是一个O，即跟随A的那个）。请注意，在同一行中，对于j = 4，我们具有值3，因为现在O的最后位置是与之相应的B中的第二个O（由于没有更多O存在，所以其余的行将为3）。
回想一下，构建P是必要的预处理步骤，如果您想轻松找到使方程式（2）的递归停止的k值。现在应该明白，P[i,j]是（3）中您要寻找的k值。使用P，您可以在O（1）的时间内确定该值。
C [i]是字母表中的一个字母-我们当前正在考虑的字母。在上面的示例中，C = [A，E，I，O，U]，C [1] = A，C [2] = E等。在等式（7）中，c是C中a（i）（当前正在考虑的字符串A的当前字母）所在的位置。这是有意义的：毕竟，在构建得分表位置S [i，j]时，我们想使用P找到k的值-我们想知道最后一次看到a（i）在j之前在B中的位置。我们通过读取P [index_of（a（i）），j]来实现这一点。P的用途，让我们看看您的实现情况。P显示为列出整个字母表的表格。遍历字母表是一个很好的主意，因为该算法的典型用途是生物信息学，其中字母表比字符串A小得多，使得遍历字母表更加便宜。C将是所有可能对象的集合，因此您必须使用所有可能对象实例（当然是无意义的）构建表格P。与您的字符串大小相比，这绝对是字母表尺寸巨大的情况。但是，请注意，您只会在与A中的字母对应的那些行中索引P：任何不在A中的字母C [i]的P中的行都是无用的，并且永远不会使用。这使您的生活更轻松，因为它意味着您可以使用字符串A而不是使用每个可能对象的字母表来构建P。AEIOU，A是EEI，B是AOOIUEI，则您仅会在E和I的行中索引P，因此您在P中只需要这些内容：P[c,j]是P中字符c的条目，而c是a(i)的索引。换句话说：C[c]总是属于A，因此为了情况下A的大小远小于C的大小的情况，构建A的字符的P比使用整个字母表更有意义。