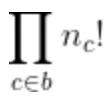本次探索的主要发现如下:
- 难度与字符串长度n无关,而是与在b中产生a的可能路径数有关(对于给定的n,可能的路径数可以从1到很多)。我们提供了一个闭合形式函数来计算路径数numpaths,它是n_c!(即factorial(n_c))的乘积,其中n_c是字符c在任一字符串中出现的次数。
- 因此,这样的潜在解决方案可能非常多。
- 在这个集合中,也可能有大量等效的解决方案(成本相同)。
- 确定某个路径是否最优(除非其成本为0)是困难的,并且需要工作。
- 在分支限界方法中,不同下限之间存在权衡,包括它们的功率(边界有多紧)和计算所需的时间。
- 没有一种单一的求解器能够支配所有其他求解器:某些优化在某些设置中表现出色,在其他设置中则表现非常差。即使是@KellyBundy的naive_memoized版本,它以节省时间为代价换取无限空间要求,在平均情况下对于m=n//2表现良好,对于m=isqrt(n)则稍逊一筹,并且在病态情况下可能比其他情况慢1000倍。
所有这些都是提示(但没有证明)问题可能是NP难题。
注意
此前版本的帖子错误地声称已经证明了NP难度。我们曾试图将问题表述为一个有向图,其中最小权重的哈密顿路径对应于我们在这里搜索的解。
首先,正如@KellyBundy和@NiceGuySaysHi正确指出的那样,这只能证明我们可以在指数时间内解决该问题。为了证明NP难度,我们需要做相反的事情:找到一个已知的NP难问题,并展示我们可以将该问题的任何实例转化为我们的问题来解决它,同时只增加输入大小的多项式表达式。
此外,正如@גלעדברקן正确指出的那样,图形过程也是错误的:尽管它可以处理简单的例子,但更大的例子会引入不需要的可能解。
因此,我纠正了错误,并完全删除了图形分析。剩下的是其他一些人发现有趣的分析部分。
概述
一些基本观察:
- 距离不对称:
dist(a, b) != dist(b, a)
- 距离与反转字符串的距离相同:
dist(a, b) == dist(r(a), r(b)),其中
r(s)是s[::-1]
- 这立即淘汰了通常的字符串距离(Levenshtein、Jaro、Jaro-Winkler、Hamming等)
建立一些直觉:
- 难度与字符串长度无关
- 什么是复杂性的好衡量?路径数量的表达式,
numpaths(b)
- 2D表示,
pos和
wheels编码
- 很难验证路径是否最小
- 很难开发一个好的下限
- 一些解算器(返回成本和找到的路径)
- 时间观察。
基本观察
首先是一个用于生成任意大小问题的工具:
def gen(n, m):
"""Generates a random problem with n chars chosen among m"""
a = ''.join(np.tile(list(ascii_letters[:m]), n // m + 1)[:n])
a = shuffle(a)
b = shuffle(a)
return a, b
>>> gen(6, 3)
('bcbaca', 'baaccb')
然后,我们还采用了@chrslg的优秀lessNaive()函数,并作出一些小的修改:
HIGHCOST = 1_000_000
HIGHSOL = HIGHCOST, tuple()
TERMSOL = (0, tuple())
def lsn2(a, b, best=HIGHCOST, prev=-1):
"""
reformulation of `lessNaive()`, eliminating `sofar` and only using `best`
"""
if not a:
return 0
if prev > 0 and best <= 1 or best <= 0:
return HIGHCOST
c, a = a[0], a[1:]
for i, bc in enumerate(b):
if c != bc:
continue
if prev > i:
res = lsn2(a, stringPop(b, i), best - 1, i) + 1
else:
res = lsn2(a, stringPop(b, i), best, i)
if res < best:
best = res
return best
现在,我们检查距离是否对称以及其他一些属性:
df = pd.DataFrame([
gen(n, (n + 1) // 2)
for n in range(3, 20)
for _ in range(100 // n)
], columns=list('ab')).drop_duplicates()
df = df.assign(
a_b=df.apply(lambda r: lsn2(r.a, r.b), axis=1),
b_a=df.apply(lambda r: lsn2(r.b, r.a), axis=1),
ra_rb=df.apply(lambda r: lsn2(r.a[::-1], r.b[::-1]), axis=1),
a_rb=df.apply(lambda r: lsn2(r.a, r.b[::-1]), axis=1),
ra_b=df.apply(lambda r: lsn2(r.a[::-1], r.b), axis=1),
).set_index(['a', 'b'])
非对称成本的例子:
>>> df[['a_b', 'b_a']].query('a_b != b_a').reset_index()
a b a_b b_a
0 bbaa abab 1 2
1 baba aabb 2 1
2 acbba bacab 1 2
.. ... ... ... ...
73 cefibfcjhdahbaedgig cebfjadidebcihhaggf 7 5
74 hebicjhgfcdfedaagbi edjcdgcbbfhiaghifea 6 7
75 bifghgecifdaachedbj ifjfcebadchgeahdgib 6 5
然而:
cols = [k for k in df.columns if k not in {'a', 'b'}]
equalities = [
f'{i} == {j}' for i, j in permutations(cols, 2)
if (df[i] == df[j]).all() and i < j
]
>>> equalities
['a_b == ra_rb', 'a_rb == ra_b']
⇒ dist(a, b) != dist(b, a), 但是dist(a, b) == dist(reverse(a), reverse(b))。
这立即淘汰了大多数常见的字符串距离(Levenshtein、Jaro、Jaro-Winkler、Hamming等),因为它们是对称的。
建立一些直觉
首先要观察的是,找到解决方案的难度并不取决于字符串的大小n。当不存在字符重复时,无论n有多大,都只有一条可能的路径。
相反,主要的困难度量是每个字符位置可用的排列数量。
让我们用可能是最低效的求解器来说明:一个遍历所有可能排列的求解器。请注意,这也可以用来检查另一个求解器的正确性(通过检查其返回的解决方案是否是可能的最小路径之一)。我们还引入了一个(显然的)成本度量,仅使用找到的路径作为输入。
但是首先,让我们介绍一种编码问题的方法,使一些分析变得更容易:
def encode(s):
"""encode a string as a dict: {c: i}"""
d = {}
for i, c in enumerate(s):
d[c] = d.get(c, tuple()) + (i, )
return d
def encode_as_wheels(a, b):
"""
Encodes a problem as: pos, wheels.
For each character at position `i` in `a`, that character can
be found in `b` at indices `wheels[pos[i]]`.
Each wheel is always ordered.
Example:
>>> encode_as_wheels('aba', 'baa')
((1, 0, 1), ((0,), (1, 2)))
"""
wheels = {}
for i, c in enumerate(b):
wheels[c] = wheels.get(c, tuple()) + (i, )
rw = {c: i for i, c in enumerate(wheels)}
pos = tuple(rw[c] for c in a)
wheels = tuple(wheels.values())
return pos, wheels
有了这个,下面是“by_permutation”求解器:
def compute_cost(seq):
return sum([i > j for i, j in zip(seq, seq[1:])])
def by_permutation(pos, wheels):
slots = [v for _, v in sorted(encode(pos).items())]
for val in product(*[permutations(w) for w in wheels]):
seq = [(i, j) for ii, jj in zip(slots, val) for i, j in zip(ii, jj)]
seq = [v for _, v in sorted(seq)]
yield compute_cost(seq), seq
这里是一个简单的例子:
>>> list(by_permutation(*encode_as_wheels('abacb', 'bacab')))
[(2, [1, 0, 3, 2, 4]),
(1, [3, 0, 1, 2, 4]),
(3, [1, 4, 3, 2, 0]),
(2, [3, 4, 1, 2, 0])]
在这种情况下,有一条成本为1的最优路径([3, 0, 1, 2, 4]),两条成本为2的路径和一条成本为3的路径。
让我们比较两个问题:
n=15, m=15 和
n=15, m=4。
a, b = 'fdombcglihaeknj', 'clbjmohagfdeink'
n, m = len(a), len(set(list(a)))
>>> n, m
(15, 15)
sol = list(by_permutation(*encode_as_wheels(a, b)))
best = min(sol)
>>> best
(8, [9, 10, 5, 4, 2, 0, 8, 1, 12, 6, 7, 11, 14, 13, 3])
>>> len(sol)
1
相比之下:
a, b = 'dabacbbcadccbad', 'baccddcaadbbcab'
n, m = len(a), len(set(list(a)))
>>> n, m
(15, 4)
sol = list(by_permutation(*encode_as_wheels(a, b)))
best = min(sol)
>>> best
(4, [4, 7, 0, 1, 2, 10, 11, 3, 13, 5, 6, 12, 14, 8, 9])
>>> len(sol)
82944
>>> len([s for s in sol if s[0] == best[0]])
600
难度的度量
如果n不能反映问题的难度,那么是什么?从上面的by_permutation函数,我们看到b中路径的数量为:
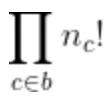
其中n_c表示在b中出现字符c的次数。
它只与b(或a,因为每个字符串中的n_c相同)有关。因此我们可以以闭合形式计算出来:
from math import factorial
from collections import Counter
def numpaths(b):
cnt = Counter(b)
np = 1
for k in cnt.values():
np *= factorial(k)
return np
以上是示例:
a, b = 'fdombcglihaeknj', 'clbjmohagfdeink'
>>> numpaths(b)
1
a, b = 'dabacbbcadccbad', 'baccddcaadbbcab'
>>> numpaths(b)
82944
>>> numpaths(a)
82944
请注意,当字符在
b中连续时,它们不应该以多种方式尝试。一些求解器(例如
lsn3)探索了这一点,但并非所有求解器都这样做。因此,我们认为路径数是问题的
基本难度的良好估计,当然,启发式算法(简单或更复杂)可以缩小路径数。
因此,这个数字可能是用作时间测量x轴的更好的度量标准。如果时间允许,我们将根据该数字重新审视下面的时间测量部分。
使用
pos和
wheels编码的2D表示
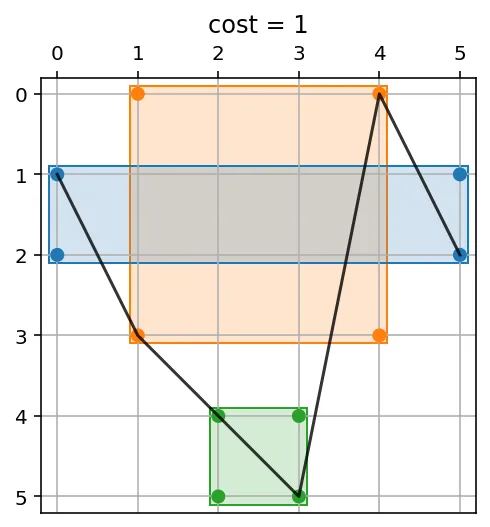
为了理解难度,我们构建了
plot_wheels()(稍后发布)。其解释是:每个字符都有自己的颜色,在
a[x]和
b[y]中存在字符的位置上有点。一个求解器(默认为
xlsn2)找到的最优路径被绘制为黑线:
a, b = gen(6, 3)
>>> a, b
('cabbac', 'accabb')
plot_wheels(*encode_as_wheels(a, b))
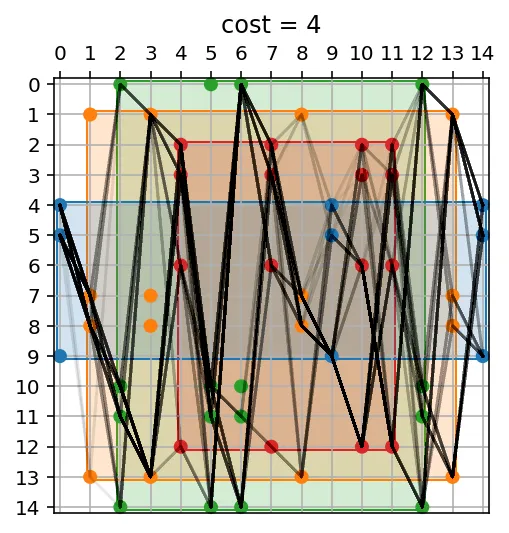
让我们看一下之前的情况,我们找到了600个等效解。我们还指定了解决方案求解器为按排列计算,这样我们就可以看到所有等效的解(所有最小成本的600个):
a, b = 'dabacbbcadccbad', 'baccddcaadbbcab'
plot_wheels(*encode_as_wheels(a, b), sol=by_permutation)
我们目前的主要发现如下:
- 由于它们的组合性质,可能会有大量的潜在解决方案。
- 在这个集合中,也可能存在大量等效的解决方案(成本相同)。
- 除非其成本为0,否则决定路径是否最优是困难的并需要工作。
所有这些都是问题“可能”是NP难的提示(但没有证明)。
难以确定路径是否最小
在我写这篇答案的有趣时光中,我尝试了许多优化/启发式方法来进一步消除分支。我发现很难确定路径是否最优。而且很容易开发一个看似很好的“下界”,可以减少很多工作并显著加快搜索速度,只是后来发现(感谢“perfplot”的“equality_check”),它是错误的,并且存在一些边角情况,导致实际路径的成本低于(错误的)下界规定的成本。
也许这种难度(难以确定路径是否最优)是证明NP难度的一条途径?
求解器
我写了几个求解器。有些是基于 pos, wheels 参数工作的,而另一些则直接处理字符串 a, b。有些具有强大的回溯剪枝 lowerbound 估计,而其他一些则追求简单(它们回溯更多,但通常净效果相当,因为它们每个路径需要做的工作要少得多)。
在这里,我将介绍一个非常快速的求解器(在某些情况下比 lessNaive 或 lsn2 快100倍),并且还会返回找到的路径及其成本:
def xlsn3(a, b, best=HIGHCOST, prev=-1):
"""
When encountering consecutive letters in b, no need to backtrack
"""
mincost = int(prev > 0)
if a == b:
return mincost, tuple(range(len(a)))
if best <= mincost:
return HIGHSOL
c, a = a[0], a[1:]
bestseq = tuple()
i0 = max(prev, 0)
j = -2
for i, bc in chain(enumerate(b[i0:], i0), enumerate(b[:i0])):
if c != bc:
continue
if i - j != 1:
deltacost = int(prev > i)
cost, seq = xlsn3(a, stringPop(b, i), best - deltacost, i)
cost += deltacost
if cost < best:
best = cost
bestseq = (i,) + seq
if best <= mincost:
return best, adjust_seq(bestseq)
j = i
return best, adjust_seq(bestseq)
def adjust_seq(seq):
if len(seq) < 2:
return seq
y = seq[0]
return (y,) + tuple(e + (e >= y) for e in seq[1:])
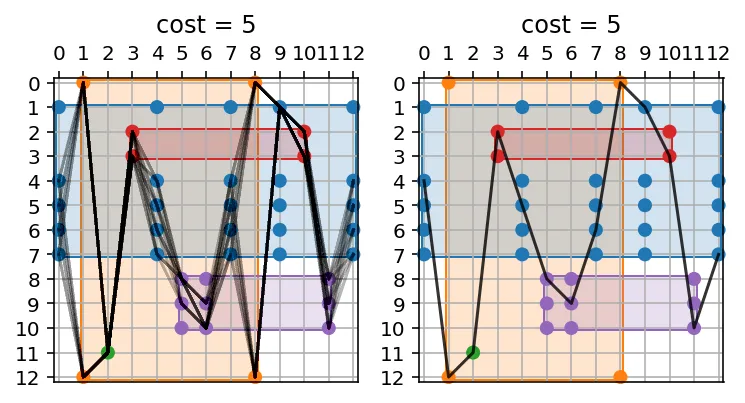
这个问题的特殊之处在于一种优化,看起来可以简单地减少许多组合:当两个或更多字母在
b中连续时,尝试它们的反向是没有意义的。只有按顺序使用它们,我们仍然保证找到最佳路径,因为先“消耗”高位置再消耗较低位置不会有任何收益。
让我们看一个例子:
b = 'abccbbbbdddea'
a = shuffle(b)
>>> a, b
('baecbddbabcdb', 'abccbbbbdddea')
fig, axes = plt.subplots(ncols=2)
plot_wheels(*encode_as_wheels(a, b), sol=by_permutation, ax=axes[0])
plot_wheels(*encode_as_wheels(a, b), sol=xlsn3(a, b), ax=axes[1])
计时
我们使用优秀的perfplot来绘制一些算法的性能。在本文中,我只介绍了lsn2和xlsn3。基本上,lsn2与@chrlsg的lessNaive函数相同(在性能图中几乎无法区分,因此我在此处将其删除)。lsn3是xlsn3的仅返回成本的表亲。我们开发了许多其他函数,这里没有展示,具有各种启发式方法以安全地丢弃子分支。其中一些启发式方法通常是各种复杂度的下限,它们使我们放弃不可能产生成本改进的子分支。权衡是截止值的强度(对于给定问题,我们会遭受多少递归)与额外花费在计算界限本身的时间之间。
我们还添加了@KellyBundy的LRU缓存版本OP的“naive”求解器:
naive_memoized。这可以通过简单地记住在解决问题的过程中已经探索过的相同子分支来降低时间要求,带来一定的空间(内存)开销。请注意,在
naive_memoized内设置新缓存函数的正确实现,以便重复计时不会仅仅记住以前运行的数据。
关于时间的一个重要问题是,对于给定的
n,复杂度可能会有很大的变化(正如上面所述,因为真正的难点来自可能的排列数)。因此,我们使用一些循环来重复测量
perfplot 的运行时间,并绘制这些运行的平均值。
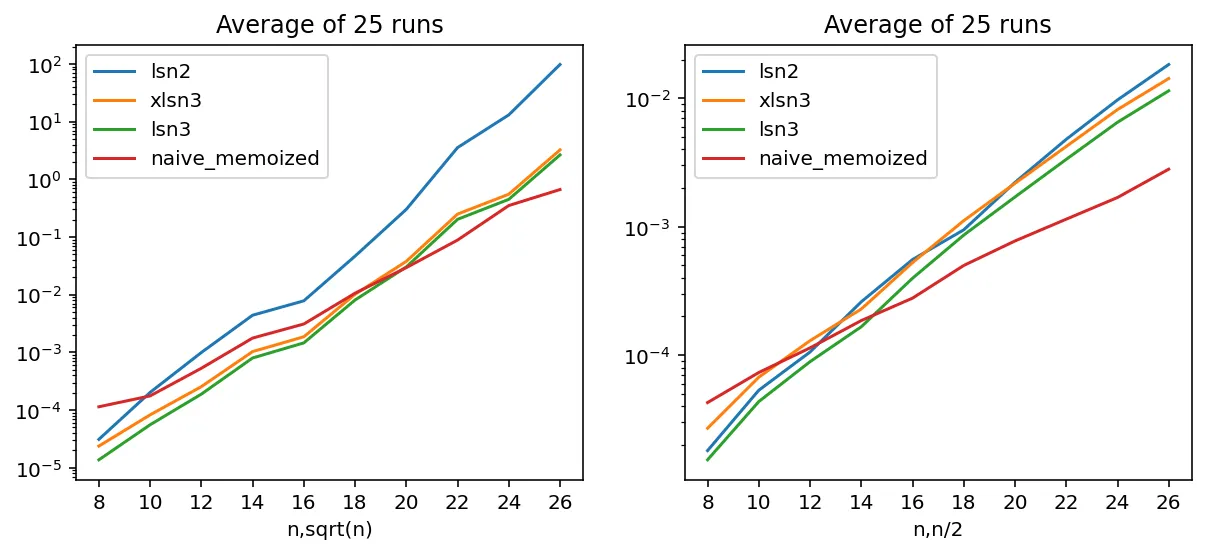
关于naive_memoized的注意事项:通过以时间换取无限制的内存,这个求解器在m=n//2的情况下表现良好,但对于m=isqrt(n)的情况则不太理想(尽管在半对数图中其斜率仍然更好)。
此外,在某些情况下,它的性能可能比lsn3慢1000倍。例如:
a, b = 'bbaababaababaaabbba', 'abbabaaababaabbbaab'
tmem = %timeit -o naive_memoized(a, b)
tln3 = %timeit -o lsn3(a, b)
>>> tmem.average / tln3.average
1052.6