有理数是可枚举的。例如,这段代码可以找到0..1开区间内按照排序顺序排列的第k个有理数,其中假设{n1, d1}在{n2, d2}之前,如果(d1<d2 || (d1==d2 && n1<n2)),那么{n,d}是互质的。
RankedRational[i_Integer?Positive] :=
Module[{sum = 0, eph = 1, den = 1},
While[sum < i, sum += (eph = EulerPhi[++den])];
Select[Range[den - 1], CoprimeQ[#, den] &][[i - (sum - eph)]]/den
]
In[118]:= Table[RankedRational[i], {i, 1, 11}]
Out[118]= {1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 5/6}
现在我想要生成随机有理数,给定一个上限分母,使得对于足够大的分母有理数在单位区间上是均匀分布的。为了达到这个目的,我们可以直觉地从所有具有较小分母的有理数中等权重地选择:
RandomRational1[maxden_, len_] :=
RandomChoice[(Table[
i/j, {j, 2, maxden}, {i,
Select[Range[j - 1], CoprimeQ[#, j] &]}] // Flatten), len]
有没有更高效的方法,可以按此分布生成随机分数,而不必构造所有分数?因为这个表很容易变得非常庞大。
In[197]:= Table[RankedRational[10^k] // Denominator, {k, 2, 10}]
Out[197]= {18, 58, 181, 573, 1814, 5736, 18138, 57357, 181380}
也许有可能高效地生成分母受限的有不同“感觉均匀”分布的有理数?
编辑这是运行btilly建议的接受-拒绝生成的Mathematica代码。
Clear[RandomFarey];
RandomFarey[n_, len_] := Module[{pairs, dim = 0, res, gcds},
Join @@ Reap[While[dim < len,
gcds = cfGCD[pairs = cfPairs[n, len - dim]];
pairs = Pick[pairs, gcds, 1];
If[pairs =!= {},
dim += Length@Sow[res = pairs[[All, 1]]/pairs[[All, 2]]]];
]][[2, -1]]
]
{i,j},满足1≤i:cfPairs =
Compile[{{n, _Integer}, {len, _Integer}},
Table[{i, RandomInteger[{i + 1, n}]}, {i,
RandomChoice[2 (n - Range[n - 1])/(n (n - 1.0)) -> Range[n - 1],
len]}]];
以下编译函数计算最大公约数,假设输入为两个正整数。
cfGCD = Compile[{{prs, _Integer, 1}}, Module[{a, b, p, q, mod},
a = prs[[1]]; b = prs[[2]]; p = Max[a, b]; q = Min[a, b];
While[q > 0, mod = Mod[p, q]; p = q; q = mod]; p],
RuntimeAttributes -> Listable];
In[151]:= data = RandomFarey[12, 10^6]; // AbsoluteTiming
Out[151]= {1.5423084, Null}
In[152]:= cdf = CDF[EmpiricalDistribution[data], x];
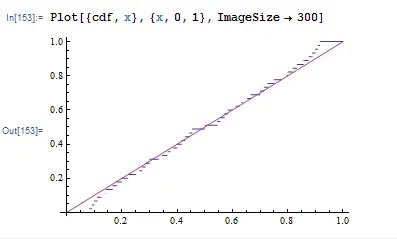
In[153]:= Plot[{cdf, x}, {x, 0, 1}, ImageSize -> 300]