如何在不实际转换和计算的情况下获取一个数字的二进制表示中 “1”的数量？
例如：
def number_of_ones(n):
# do something
# I want to MAKE this FASTER (computationally less complex).
c = 0
while n:
c += n%2
n /= 2
return c
>>> number_of_ones(5)
2
>>> number_of_ones(4)
1
我不是Python程序员，但希望这对你有所帮助。
c = 0
while n:
c += 1
n &= n - 1
return c
虽然有点晦涩，但它的主要优势是速度和简洁性。while循环仅在n中设置为1的位数上迭代一次。
在我看来，一个好的方法是使用查找表-创建一个将字节转换为1的数量的字典（您可以使用您发布的代码生成它，只需要运行一次），然后使用类似以下内容的东西：
def number_of_ones(n):
sum = 0
while n != 0:
sum += lookup_table[n & 0xff]
n >>= 8
return sum
如果你想在一行代码中完成，你可以使用以下方法：
sum( [x&(1<<i)>0 for i in range(32)] )
Hamming weight是用于计算二进制数中1的个数的算法。
以下是一个时间复杂度为O(log(n))（n为位数）的解决方案：
m1 = 0x5555555555555555 #binary: 0101...
m2 = 0x3333333333333333 #binary: 00110011..
m4 = 0x0f0f0f0f0f0f0f0f #binary: 4 zeros, 4 ones ...
m8 = 0x00ff00ff00ff00ff #binary: 8 zeros, 8 ones ...
m16 = 0x0000ffff0000ffff #binary: 16 zeros, 16 ones ...
m32 = 0x00000000ffffffff #binary: 32 zeros, 32 ones
h01 = 0x0101010101010101 #the sum of 256 to the power of 0,1,2,3...
def hammingWeight(x: int) -> int:
x -= (x>>1)&m1
x = (x&m2) + ((x>>2)&m2)
x = (x+(x>>4))&m4
return ((x*h01)>>56)&0x7f
bit_count()在清晰度和性能方面都要好得多。 - Peter Cordesdef bitCount(int_no):
c = 0
while(int_no):
int_no &= (int_no - 1)
c += 1
return c
如果你真的关心速度，用C语言编写代码（参见this question），并使用类似于ctypes的东西与C实现进行接口交互。
p = lambda n:n and 1+p(n&(n-1))
这个程序使用了短路和递归，当n大于0时，它会切换到计算1+p(n&(n-1))，其中调用了p(n&(n-1))等等，当n为0时返回0。复杂度为O(n)，因为它运行的次数是二进制中存在的1的数量。
例如：p(9) = 1+p(8) = 1+1+p(0) = 1+1+0=2
我今天来这里是为了检查现有技术的状态。
这是一个时常出现的话题，现代CPU有人口统计算法。这对于在某些通信应用程序中计算 Bit Error Rate 很有用。这是汉明重量，与 Hamming Distance 相关，Scipy 有一个 实现，但它使用数组而不是数字的二进制表示进行计算。对于固定大小的计算，例如 numpy 数组，我知道的最快方法是 此回答中的方法，但是所述方法，我将其称为分而治之的方法。在一般情况下，分而治之的复杂度为 O(log(n)) 而不是 O(n)。对于大多数情况，接受的答案非常好，甚至在诸如 C 这样的语言中更好，您可以简单地取((*char)bits)[i]，而无需移动数字。
def dq_number_of_ones(n):
nb = 1
while n >> nb:
nb *= 2
t = (1 << nb) - 1
masks = []
while nb > 1:
nb //= 2
t ^= t >> nb
masks.append(t)
t = n
s = 1
for tm in masks[::-1]:
tm = masks.pop()
t = ((tm & t) >> s) + ((tm >> s) & t)
s *= 2
return t
为了完整性，这里展示原帖的方法和被接受的查找表方法
def number_of_ones(n):
# do something
# I want to MAKE this FASTER (computationally less complex).
c = 0
while n:
c += n%2
n //= 2
return c
lookup_table = [number_of_ones(i) for i in range(256)]
def lt_number_of_ones(n):
sum = 0
while n != 0:
sum += lookup_table[n & 0xff]
n >>= 8
return sum
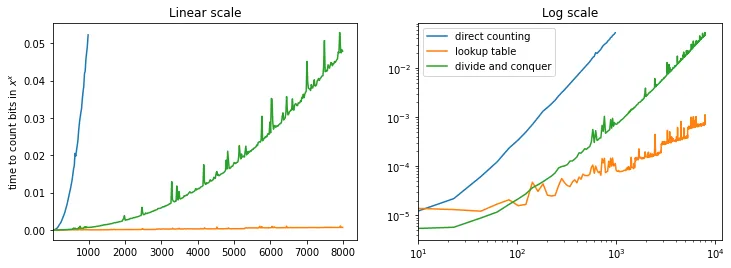
这是两者的实际比较
import time
import matplotlib.pyplot as plt
x = []
t1 = []
t2 = []
t3 = []
for i in range(3,8000,20):
y = i**i
if i < 1000:
time.sleep(0.0001)
t0 = time.time()
w1 = number_of_ones(y)
t1.append(time.time() - t0)
else:
t1.append(np.nan)
time.sleep(0.0001)
t0 = time.time()
w2 = dq_number_of_ones(y)
t2.append(time.time() - t0)
time.sleep(0.0001)
t0 = time.time()
_ = lt_number_of_ones(y)
t3.append(time.time() - t0)
time.sleep(0.0001)
x.append(i)
plt.figure(figsize=(12, 4))
plt.subplot(121)
plt.plot(x, t1)
plt.plot(x, t2)
plt.plot(x, t3)
plt.xlim([10,None])
plt.title('Linear scale')
plt.ylabel('time to count bits in $x^x$')
plt.subplot(122)
plt.loglog(x, t1)
plt.loglog(x, t2)
plt.loglog(x, t3)
plt.xlim([10,None])
plt.title('Log scale')
plt.legend(['direct counting', 'lookup table', 'divide and conquer'])
0x5555555555555555）的策略最好被描述为 SWAR 位操作技巧。（如在在32位整数中计算设置位的数量中所述）。我猜分而治之也有点合适，因为你要将其分成2位累加器并扩展。然而，该版本仅适用于64位整数及更窄的版本。在程序中有时使用大整数的情况下，可以检查大小是否更大。我认为与内置的bit_count()相比，这些都非常慢，希望内置函数能够使这些过时。 - Peter Cordesn &= n - 1 的迭代次数（通常归因于Kernighan）是另一个值得关注的算法，适用于只有少量设置位的数字。 - Peter Cordes
def bitCount(int_no):
if not isinstance( int_no, int) or int_no < 0:
return None
count = 0
while(int_no):
int_no &= (int_no - 1)
count += 1
return count
from math import floor, log
def bitsSet(int_no):
if not isinstance( int_no, int) or int_no < 0:
return None
bit_indexes = []
while(int_no):
index = floor(log(int_no, 2))
int_no &= (pow(2, index) - 1)
bit_indexes.insert(0, index)
return bit_indexes
int.bit_count()函数。 - Peter Cordes